试题分析:作底边上的高AD,设BP=xcm,根据等腰三角形三线合一的性质可得AD=3,在Rt△APD中,根据勾股定理可得AP
2=PD
2+AD
2=(4-x)
2+3
2,在Rt△APC中,根据勾股定理可得AP
2+AC
2=PC
2,即可得到关于x的方程,求得x的值,从而可得BP的长,求得P点移动的时间,再得到得P的对称点P′,即可求得BP′的长,从而求得P点移动的时间.
作底边上的高AD

设BP=xcm
易得AD=3
在Rt△APD中
AP
2=PD
2+AD
2=(4-x)
2+3
2在Rt△APC中 ,
AP
2+AC
2=PC
2∴(4-x)
2+3
2+5
2=(8-x)
2得x=

∴BP=

∴P点移动时间为

÷0.25=7(s)
易得P的对称点P′,即BP′=8-

=

即

÷0.25=25(s)
∴当P点运动7s或25s时,PA与腰垂直。
点评:此题综合性较强,难度较大,注意掌握辅助线的作法是解此题的关键,注意数形结合思想与方程思想的应用.





 ÷0.25=7(s)
÷0.25=7(s) =
=
 ÷0.25=25(s)
÷0.25=25(s)

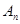 与∠
与∠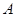 的关系式。
的关系式。