
分析 由点A、B在反比例函数$y=\frac{-2}{x}$的图象上,可得出b1=$\frac{-2}{{a}_{1}}$,b2=$\frac{-2}{{a}_{2}}$,再根据a1<$a_2^{\;}$<0可得出$\frac{-2}{{a}_{1}}$<$\frac{-2}{{a}_{2}}$,从而得出b1<b2.
解答 解:∵点A(a1,b1),点B(a2,b2)在反比例函数$y=\frac{-2}{x}$的图象上,
∴b1=$\frac{-2}{{a}_{1}}$,b2=$\frac{-2}{{a}_{2}}$,
又∵a1<$a_2^{\;}$<0,
∴$\frac{-2}{{a}_{1}}$<$\frac{-2}{{a}_{2}}$,
∴b1<b2.
故答案为:<.
点评 本题考查了反比例函数图象上点的坐标特征,解题的关键是找出$\frac{-2}{{a}_{1}}$<$\frac{-2}{{a}_{2}}$.本题属于基础题,难度不大,解决该题型题目时,借助于反比例函数的单调性更简便.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A,F,E,C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知A,F,E,C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组,并把它们的解集在数轴上表示出来:
解不等式组,并把它们的解集在数轴上表示出来:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
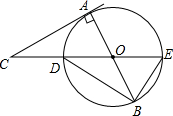 已知,如图,AB是⊙O的直径,CA与⊙O相切于点A,连接CO交⊙O于点D,CO的延长线交⊙O于点E,连接BE、BD,∠ABD=35°,则∠C=20度.
已知,如图,AB是⊙O的直径,CA与⊙O相切于点A,连接CO交⊙O于点D,CO的延长线交⊙O于点E,连接BE、BD,∠ABD=35°,则∠C=20度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com