Question

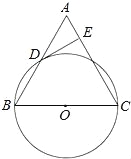
【题目】已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．

（1）求证：点D是AB的中点；

（2）判断DE与⊙O的位置关系，并证明你的结论；

（3）若⊙O的直径为18，cosB=，求DE的长．

Answer 1

【答案】（1）（2）DE是⊙O的切线（3）

【解析】

试题分析：（1）连接CD，由BC为直径可知CD⊥AB，又BC=AC，由等腰三角形的底边“三线合一”证明结论；

（2）连接OD，则OD为△ABC的中位线，OD∥AC，已知DE⊥AC，可证DE⊥OC，证明结论；

（3）连接CD，在Rt△BCD中，已知BC=18，cosB=，求得BD=6，则AD=BD=6，在Rt△ADE中，已知AD=6，cosA=cosB=，可求AE，利用勾股定理求DE．

试题解析：（1）连接CD，

∵BC为⊙O的直径，∴CD⊥AB，

又∵AC=BC，

∴AD=BD，即点D是AB的中点．

（2）DE是⊙O的切线．

证明：连接OD，则DO是△ABC的中位线，

∴DO∥AC，

又∵DE⊥AC，

∴DE⊥DO即DE是⊙O的切线；

（3）∵AC=BC，∴∠B=∠A，

∴cosB=cosA=，

∵cosB=，BC=18，

∴BD=6，

∴AD=6，

∵cosA=，

∴AE=2，

在Rt△AED中，DE=．