Question

7．如图，△ABC内接于⊙O，直径DE⊥AB于点F，交BC于点 M，DE的延长线与AC的延长线交于点N，连接AM． 
（1）求证：AM=BM；
（2）若AM⊥BM，DE=8，∠N=15°，求BC的长．

Answer 1

分析 （1）由垂径定理可求得AF=BF，可知DE为AB的垂直平分线，可得AM=BM；
（2）连接AO，BO，可求得∠ACB=60°，可求得∠AOF，由DE的长可知AO，在Rt△AOF中得AF，在Rt△AMF中可求得AM，在Rt△ACM中，由$tan∠ACM=\frac{AM}{CM}$，可求得CM，则可求得BC的长．

解答 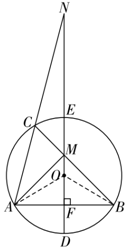（1）证明：
∵直径DE⊥AB于点F，
∴AF=BF，
∴AM=BM；
（2）连接AO，BO，如图，
由（1）可得 AM=BM，
∵AM⊥BM，
∴∠MAF=∠MBF=45°，
∴∠CMN=∠BMF=45°，
∵AO=BO，DE⊥AB，
∴∠AOF=∠BOF=$\frac{1}{2}∠AOB$，
∵∠N=15°，
∴∠ACM=∠CMN+∠N=60°，即∠ACB=60°，
∵∠ACB=$\frac{1}{2}∠AOB$．
∴∠AOF=∠ACB=60°．
∵DE=8，
∴AO=4．
在Rt△AOF中，由$sin∠AOB=\frac{AF}{AO}$，得AF=$2\sqrt{3}$，
在Rt△AMF中，AM=BM=$\sqrt{2}AF$=$2\sqrt{6}$．
在Rt△ACM中，由$tan∠ACM=\frac{AM}{CM}$，得CM=$2\sqrt{2}$，
∴BC=CM+BM=$2\sqrt{2}$+$2\sqrt{6}$．

点评 本题主要考查圆周角定理、垂径定理，在（2）中注意在不同的直角三角形中利用勾股定理是解题的关键．