
 如图,在长方形ABCD中,AB=10厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:
如图,在长方形ABCD中,AB=10厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:分析 (1)由题意表示出:AP=2t,DQ=t,则AQ=6-t,并根据AP=AQ列等式解出t的值;
(2)由矩形的性质可知:△AQB是直角三角形,根据面积公式表示面积;
(3)根据已知列等式求解.
解答 解:(1)由题意得:AP=2t,DQ=t,则AQ=6-t,
当AP=AQ时,2t=6-t,
t=2;
故答案为:2t,6-t;
(2)S△AQB=$\frac{1}{2}$AB•AQ=$\frac{1}{2}$×10(6-t)=-5t+30(0≤t≤6);
(3)由已知得:S△AQB=$\frac{1}{3}$S长方形ABCD,
-5t+30=$\frac{1}{3}$×10×6,
t=2,
答:若△QAB的面积等于长方形面积的$\frac{1}{3}$,t的值是2秒.
点评 本题考查了矩形的性质、三角形面积和矩形面积以及动点运动问题,此类题首先要明确动点运动的路线、速度、时间,根据路程=时间×速度表示行动的路程,再利用已知条件列等式解决问题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
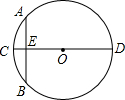 “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( )
“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( )| A. | 12寸 | B. | 13寸 | C. | 24寸 | D. | 26寸 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a2=b2,则a=b | |
| B. | 等角的余角相等 | |
| C. | 同旁内角相等,两直线平行 | |
| D. | $\overline{{x}_{A}}$=$\overline{{x}_{B}}$,SA2>SB2,则A组数据更稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读解题过程,回答问题.
阅读解题过程,回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点 M,DE的延长线与AC的延长线交于点N,连接AM.
如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点 M,DE的延长线与AC的延长线交于点N,连接AM. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com