
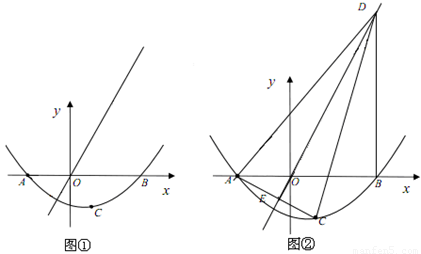
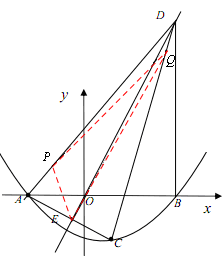
如图①,若二次函数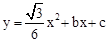 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数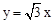 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数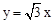 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数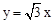 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
(1)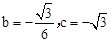 。
。
(2)利用轴对称和锐角三角函数求出点C的坐标,代入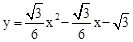 验证即可。
验证即可。
(3)存在时刻 ,使PE平分∠APQ,同时QE平分∠PQC。
,使PE平分∠APQ,同时QE平分∠PQC。
【解析】
分析:(1)将A(-2,0),B(3,0)两点坐标 代入 ,即可求出b、c的值。
,即可求出b、c的值。
(2)利用轴对称和锐角三角函数求出点C的坐标,代入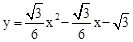 验证即可。
验证即可。
(3)通过证明△PAE∽△ECQ,求出时间t。
解:(1)∵二次函数 的图象与x轴交于点A(-2,0),B(3,0)两点,
的图象与x轴交于点A(-2,0),B(3,0)两点,
∴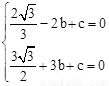 ,解得
,解得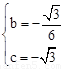 。
。
∴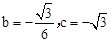 。
。
(2)证明:由(1)得二次函数解析式为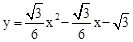 。
。
在正比例函数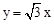 的图象上取一点F
的图象上取一点F ,作FH⊥x轴于点H,则
,作FH⊥x轴于点H,则
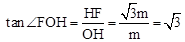 。∴
。∴ 。
。
连接AC交
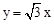 的图象于点E,作CK 垂直x轴于点K,
的图象于点E,作CK 垂直x轴于点K,
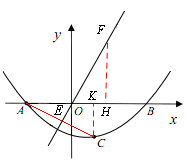
∵点A关于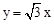 的图象的对称点为C,
的图象的对称点为C,
∴OE垂直平分AC。
∵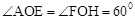 ,OA=2,
,OA=2,
∴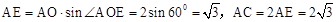 。
。
在Rt△ACK中,∵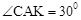 ,
,
∴ 。∴
。∴ 。
。
∴点C 的坐标为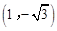 。
。
将C 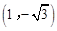 代入
代入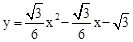 ,左边=右边,
,左边=右边,
∴点C在所求的二次函数的图象上。
(3)∵DB⊥x轴交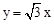 的图象于点D,B(3,0),
的图象于点D,B(3,0),
∴把x=3代入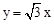 得
得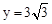 ,即BD=
,即BD=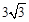 。
。
在Rt△ACK中,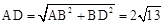 ,
,
∵OE垂直平分AC,
∴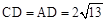 ,
, 。
。
假设存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,
则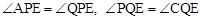 。
。
∵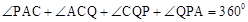 ,
∴
,
∴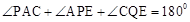 。
。
又∵ ,∴
,∴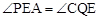 。
。
又∵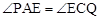 ,∴△PAE∽△ECQ。∴
,∴△PAE∽△ECQ。∴ ,即
,即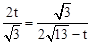 。
。
整理,得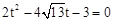 ,解得
,解得 (不合题意,舍去)。
(不合题意,舍去)。
∴存在时刻 ,使PE平分∠APQ,同时QE平分∠PQC。
,使PE平分∠APQ,同时QE平分∠PQC。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2006•河北区一模)如图,已知二次函数的顶点坐标为(2,0),直线y=x+2与该二次函数的图象交于A,B两点,其中A点在y轴上,
(2006•河北区一模)如图,已知二次函数的顶点坐标为(2,0),直线y=x+2与该二次函数的图象交于A,B两点,其中A点在y轴上,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).| 6 |
| 7 |
| 6 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
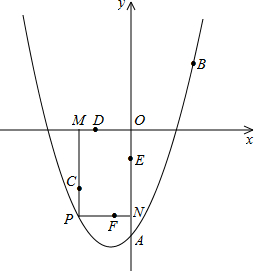 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B(| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2013年湖南省常德市中考数学试卷(解析版) 题型:解答题
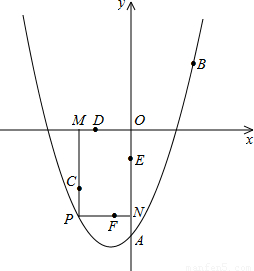 如图,已知二次函数的图象过点A(0,-3),B(
如图,已知二次函数的图象过点A(0,-3),B(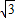 ,
,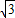 ),对称轴为直线x=-
),对称轴为直线x=- ,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=
,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC= MP,MD=
MP,MD= OM,OE=
OM,OE= ON,NF=
ON,NF= NP.
NP.查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省张家港市九年级第一学期调研试卷数学卷 题型:解答题
(本题3分+3分+4分)如图,已知二次函数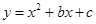 的图象与x轴交于A、B两点,与y轴交于点P,顶点为C(
的图象与x轴交于A、B两点,与y轴交于点P,顶点为C(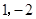 )。
)。
(1)求此函数的关系式;
(2)作点C关于x轴的对称点D,顺次连接A、C、B、D.若在抛物线上存在点E,使直线PE将四边形ACBD分成面积相等的两个四边形,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点F,使得△PEF是以P为直角顶点的直角三角形?若存在,求出点F的坐标;若不存在,请说明理由。
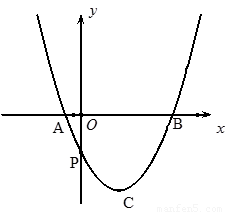
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com