
| A. | k>$\frac{1}{2}$且k≠1 | B. | k≥$\frac{1}{2}$且k≠1 | C. | k≤-$\frac{1}{2}$ | D. | k?$\frac{1}{2}$ |
分析 讨论:即k=1,方程化为一元一次方程,有一个解;当k-1≠0时,根据判别式的意义得到△=4k2-4(k-1)(k-1)≥0,解得k≥$\frac{1}{2}$,综合两种情况可得到k的范围.
解答 解:当k-1=0时,即k=1,方程化为2x=0,解得x=0;
当k-1≠0时,△=4k2-4(k-1)(k-1)≥0,解得k≥$\frac{1}{2}$,
综上所述,k的范围为k≥$\frac{1}{2}$.
故选D.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.


科目:初中数学 来源: 题型:解答题
 某课外学习小组为了了解本市城区某路段的汽车超速情况,他们在一段时间内随机测量了途径该路段汽车行驶的速度,整理并绘制出以下不完整的统计图表.
某课外学习小组为了了解本市城区某路段的汽车超速情况,他们在一段时间内随机测量了途径该路段汽车行驶的速度,整理并绘制出以下不完整的统计图表.| 数据段 | 频数 | 频率 |
| 30~40 | 10 | 0.05 |
| 40~50 | 36 | 0.18 |
| 50~60 | 78 | 0.39 |
| 60~70 | 56 | 0.28 |
| 70~80 | 20 | 0.10 |
| 总计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12.33×105 | B. | 1.233×103 | C. | 0.1233×108 | D. | 1.233×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
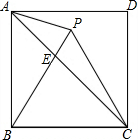 如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论:
如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com