
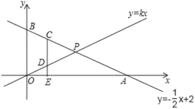
【题目】在平面直角坐标系中,一次函数![]() 的图象交
的图象交![]() 轴、
轴、![]() 轴分别于
轴分别于![]() 两点,交直线
两点,交直线![]() 于
于![]() 。
。
(1)求点![]() 的坐标;
的坐标;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,![]() 是线段
是线段![]() 上一点,
上一点,![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 点的坐标。
点的坐标。
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)分别代入x=0、y=0求出y、x的值,由此可得出点B. A的坐标;
(2)设点P的坐标为(x,y),利用一次函数图象上点的坐标特征结合等腰三角形的性质可得出点P的坐标,再由点P在直线y=kx上利用一次函数图象上点的坐标特征可求出k值;
(3)设点C的坐标为(x, ![]() x+2),则点D的坐标为(x,
x+2),则点D的坐标为(x,![]() x),点E的坐标为(x,0),进而可得出CD、DE的长度,由CD=2DE可得出关于x的一元一次方程,解之即可得出结论
x),点E的坐标为(x,0),进而可得出CD、DE的长度,由CD=2DE可得出关于x的一元一次方程,解之即可得出结论
解:(1)当![]() 时,
时,![]() ,
,
![]()
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ;
;
(2)设![]() ,因为点
,因为点![]() 在直线
在直线![]() ,且
,且![]() ,
,
![]() ,
,
把![]() 代入
代入![]() ,所以点
,所以点![]() 的坐标是
的坐标是![]() ,
,
因为点![]() 在直线
在直线![]() 上,所以
上,所以![]() ;
;
(3)设点![]() ,则
,则![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,
解得:![]() ,则
,则![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案.
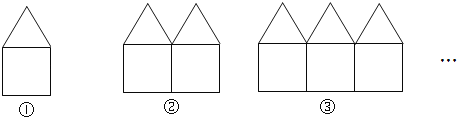
(1)第1个图案中有6根小棒;第2个图案中有 根小棒;第3个图案中有 根小棒;
(2)第n个图案中有多少根小棒?
(3)第25个图案中有多少根小棒?
(4)是否存在某个符合上述规律的图案,由2032根小棒摆成?如果有,指出是滴几个图案;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
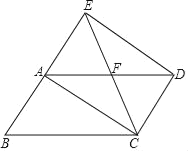
【题目】已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接CE、DE、AC,CE与AD交于点F.
(1)求证:四边形ACDE是平行四边形;
(2)若∠AFC=2∠B.求证:四边形ACDE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据绝对值定义,若有![]() ,则
,则![]() 或
或![]() ,若
,若![]() ,则
,则![]() ,我们可以根据这样的结论,解一些简单的绝对值方程,例如:
,我们可以根据这样的结论,解一些简单的绝对值方程,例如:![]()
解:方程![]() 可化为:
可化为:
![]() 或
或![]()
当![]() 时, 则有:
时, 则有:![]() ; 所以
; 所以 ![]() .
.
当![]() 时, 则有:
时, 则有:![]() ;所以
;所以 ![]() .
.
故,方程![]() 的解为
的解为![]() 或
或![]() 。
。
(1)解方程:![]()
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)在 (2)的条件下,若![]() 都是整数,则
都是整数,则![]() 的最大值是 (直接写结果,不需要过程).
的最大值是 (直接写结果,不需要过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
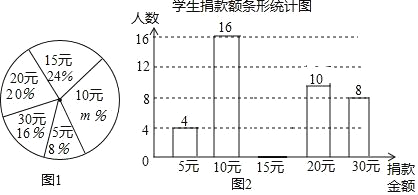
【题目】某校学生会向全校![]() 名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 人,图![]() 中
中![]() 的值是 .
的值是 .
(2)补全图2的统计图.
(3)求本次调查获取的样本数据的平均数、众数和中位数;
(4)根据样本数据,估计该校本次活动捐款金额为![]() 元的学生人数.
元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
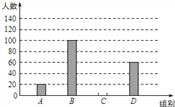
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h B组:0.5h≤t<1h C组:1h≤t<1.5h D组:t≥1.5h
请根据上述信息解答下列问题:
(1)C组的人数是 .
(2)本次调查数据的中位数落在 组内;
(3)若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
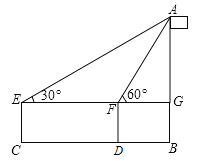
【题目】如图,小丽准备测一根旗杆AB的高度,已知小丽的眼睛离地面的距离EC=1.5米,第一次测量点C和第二次测量点D之间的距离CD=10米,∠AEG=30°,∠AFG=60°,请你帮小丽计算出这根旗杆的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产480个零件.当生产任务完成一半时,停止生产进行反思和改进,用时20分钟.恢复生产后工作效率比原来可以提高20%,要求比原计划提前40分钟完成任务,那么反思改进后每小时需要生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数小1,那么我们把这样的自然数叫做“相连数”,例如:234,4567,56789,......都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的和;
(2)若某个“相连数”恰好等于其个位数的576倍,求这个“相连数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com