
【题目】如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线l:![]() ,过点M(1,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M5的坐标为_____.
,过点M(1,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M5的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 .
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 . 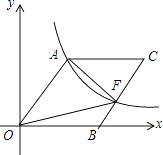
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为 ![]() m,到墙边OA的距离分别为
m,到墙边OA的距离分别为 ![]() m,
m, ![]() m.
m. 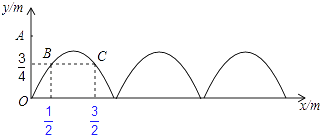
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(﹣1,m)和点B(n,5). 
(1)求该二次函数的关系式;
(2)在给定的平面直角坐标系中,画出这两个函数的大致图象;
(3)结合图象直接写出x2+bx+c>x+1时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )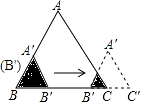
A.
B.
C.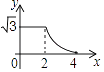
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
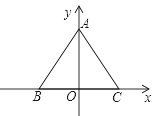
【题目】如图,已知等边△ABC的边长为a,B,C在x轴上,A在y轴上.
(1)作△ABC关于x轴的对称图形△A′B′C′;
(2)求△ABC各顶点坐标和△A′B′C′各顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是平方单位(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
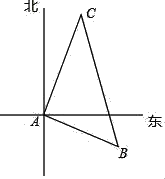
【题目】如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为4:3,货船沿东偏南10°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里.
(1)求两船的速度分别是多少?
(2)求客船航行的方向.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com