已知α+β=1,αβ=-1.设S1=α+β,S2=α2+β2,S3=α3+β3,…,Sn=αn+βn
(1)计算:S1=______,S2=______,S3=______,S4=______;
(2)试写出Sn-2、Sn-1、Sn三者之间的关系;
(3)根据以上得出结论计算:α7+β7.
解:(1)∵α+β=1,αβ=-1.
∴S
1=α+β=1.
S
2=α
2+β
2=(α+β)
2-2αβ=1+2=3.
S
3=α
3+β
3=(α+β)(α
2-αβ+β
2)=(α+β)
2-3αβ=1+3=4.
S
4=α
4+β
4=(α
2+β
2)
2-2α
2β
2=9-2=7.
故答案为:1,3,4,7;
(2)由(1)得:S
n=S
n-1+S
n-2.
证明:∵α,β是方程x
2-x-1=0的两根,
∴有:α
2=α+1,β
2=β+1,
S
n-1+S
n-2=α
n-1+β
n-1+α
n-2+β
n-2=
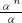
+
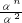
+
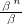
+
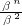
=
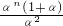
+
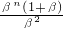
=α
n+β
n=S
n.
故S
n=S
n-1+S
n-2.
(3)由(2)有:
α
7+β
7=S
7=S
6+S
5=S
5+S
4+S
4+S
3=S
4+S
3+2S
4+S
3=3S
4+2S
3=3×7+2×4
=29.
分析:(1)运用完全平方公式和立方和公式进行计算,求出S
1,S
2,S
3,S
4的值.
(2)利用(1)中S
2=3,S
3=4,S
4=7,猜想S
n=S
n-1+S
n-2,然后由α,β是方程x
2-x-1=0的两根,得到α
2=α+1,β
2=β+1进行证明.
(3)根据(2)中的猜想得到上式为S
7=S
6+S
5进行计算求出式子的值.
点评:本题考查的是整式的混合运算,(1)题运用乘法公式计算求出S
1,S
2,S
3,S
4的值.(2)题以(1)题结果为依据猜想S
n,S
n-1,S
n-2的关系,并根据α,β是方程x
2-x-1=0的两根进行证明.(3)题利用(2)题的结论进行计算求出式子的值.

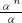 +
+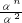 +
+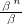 +
+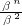
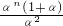 +
+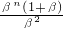


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.