
如图,点A,B分别在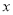 轴,
轴,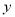 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥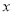 轴于点C,AO=CD=2,AB=DA=
轴于点C,AO=CD=2,AB=DA=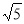 ,反比例函数
,反比例函数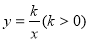 的图象过CD的中点E。
的图象过CD的中点E。
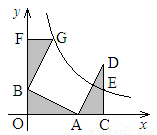
(1)求证:△AOB≌△DCA;
(2)求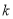 的值;
的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在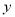 轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
(1)证明见解析
(2)K=3
(3)点G在反比例函数图象上
【解析】
试题分析:(1)利用HL可证△AOB≌△DCA
由勾股定理可求出AC的长,从而得到OC的长,可得E坐标,代入即得
(3)由△BFG和△DCA关于某点成中心对称可知BF=DC=2,FG=AC=1,从而可得点G坐标,代入判断即可
试题解析:(1)∵点A,B分别在X,Y轴上,DC⊥X轴于点C
∴∠AOB=∠DCA=90°
∵AO=CD=2,AB=DA=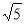
∴△AOB≌△DCA
(2)∵∠DCA=90°,DA= ,CD=2
,CD=2
∴AC=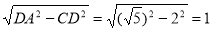
∴OC=OA+AC=2+1=3
∵E是CD的中点
∴E(3,1)
∵反比例函数 的图象过点E
的图象过点E
∴K=3
(3)∵△BFG和△DCA关于某点成中心对称
∴BF=DC=2,FG=AC=1
∵点F在Y轴上
∴OF=OB+BF=1+2=3
∴G(1,3)
把X=1代入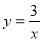 中得Y=3
中得Y=3
∴点G在反比例函数图象上
考点:1、直角三角形全等,2、勾股定理,3、反比例函数,4、中心对称


科目:初中数学 来源:2014年初中毕业升学考试(浙江湖州卷)数学(解析版) 题型:解答题
已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:选择题
下图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一个组是( )
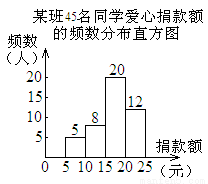
A.5~10元 B.10~15元 C.15~20元 D.20~25元
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江杭州卷)数学(解析版) 题型:选择题
已知2001年至2012年杭州市小学学校数量(单位:所)和在校学生人数(单位:人)的两幅统计图,由图得出如下四个结论:
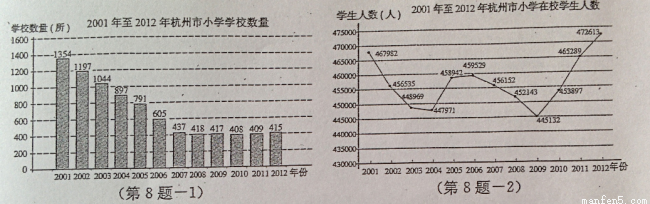
①学校数量2007至2012年比2001至2006年更稳定;
②在校学生人数有两次连续下降,两次连续增长的变化过程;
③2009年的 大于1000;
大于1000;
④2009~2012年,各相邻两年的学校数量增长和在校学生人数增长最快的都是2011~2012年.
其中,正确的结论是( )
A.①②③④ B.①②③ C.①② D.③④
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江宁波卷)数学(解析版) 题型:填空题
为解决停车难得问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出 个这样的停车位( )
)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江宁波卷)数学(解析版) 题型:选择题
如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥。如图是一个四棱柱和一个六棱锥,它们各有12条棱,下列棱柱中和九棱锥的棱数相等的是
A. 五棱柱 B. 六棱柱 C. 七棱柱 D. 八棱柱

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江西南昌卷)数学(解析版) 题型:解答题
已知梯形ABCD,请使用无刻度直尺画图.

(1)在图1中画出一个与梯形ABCD面积相等,且以CD为边的三角形;
(2)图2中画一个与梯形ABCD面积相等,且以AB为边的平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com