
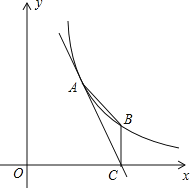
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线交反比例函数图象于点B.
(1)求反比例函数和直线AC的解析式;
(2)求△ABC的面积;
(3)在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,请直接写出符合条件的所有D点的坐标.
【答案】(1)反比例函数解析式为:y=![]() ;直线AC的解析式为:y=﹣
;直线AC的解析式为:y=﹣![]() x+8;(2)3;(3)符合条件的点D的坐标是:(3,2)或(3,6)或(9,﹣2).
x+8;(2)3;(3)符合条件的点D的坐标是:(3,2)或(3,6)或(9,﹣2).
【解析】
(1)将A点的坐标代入反比例函数y=![]() 求得k的值,然后将A,C坐标代入直线解析式解答即可;
求得k的值,然后将A,C坐标代入直线解析式解答即可;
(2)把x=6代入反比例函数解析式求得相应的y的值,即得点B的坐标,进而利用三角形面积公式解答即可;
(3)使得以A、B、C、D为顶点的四边形为平行四边形,如图所示,找出满足题意D的坐标即可.
解:(1)把点A(3,4)代入y=![]() (x>0),得
(x>0),得
k=xy=3×4=12,
故该反比例函数解析式为:y=![]() ,
,
把A(3,4),C(6,0)代入y=mx+n中,
可得:![]() ,
,
解得: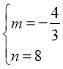 ,所以直线AC的解析式为:y=﹣
,所以直线AC的解析式为:y=﹣![]() x+8;
x+8;
(2)∵点C(6,0),BC⊥x轴,
∴把x=6代入反比例函数y=![]() ,得
,得
y=![]() =2,
=2,
则B(6,2),
所以△ABC的面积=![]() ;
;
(3)①如图,当四边形ABCD为平行四边形时,AD∥BC且AD=BC.
∵A(3,4)、B(6,2)、C(6,0),
∴点D的横坐标为3,yA﹣yD=yB﹣yC即4﹣yD=2﹣0,故yD=2.
所以D(3,2).
②如图,当四边形ACBD′为平行四边形时,AD′∥CB且AD′=CB.
∵A(3,4)、B(6,2)、C(6,0),
∴点D的横坐标为3,yD′﹣yA=yB﹣yC即yD﹣4=2﹣0,故yD′=6.
所以D′(3,6).
③如图,当四边形ACD″B为平行四边形时,AC=BD″且AC∥BD″.
∵A(3,4)、B(6,2)、C(6,0),
∴xD″﹣xB=xC﹣xA即xD″﹣6=6﹣3,故xD″=9.
yD″﹣yB=yC﹣yA即yD″﹣2=0﹣4,故yD″=﹣2.
所以D″(9,﹣2).
综上所述,符合条件的点D的坐标是:(3,2)或(3,6)或(9,﹣2).


科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
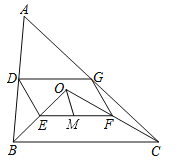
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
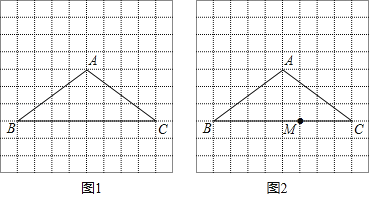
【题目】如图,10×10的网格中,A,B,C均在格点上,诮用无刻度的直尺作直线MN,使得直线MN平分△ABC的周长(留作图痕迹,不写作法)
(1)请在图1中作出符合要求的一条直线MN;
(2)如图2,点M为BC上一点,BM=5.请在AB上作出点N的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O的半径为5cm,弦AB//CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
A. 1 cm B. 7cm C. 3 cm或4 cm D. 1cm 或7cm
查看答案和解析>>
科目:初中数学 来源: 题型:
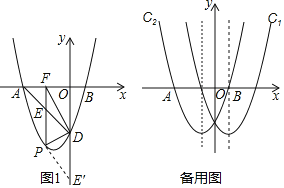
【题目】在同一直角坐标系中,抛物线C1:![]() 2
2![]() 与抛物线C2:
与抛物线C2:![]() 2
2![]() 关于
关于![]() 轴对称,C2与
轴对称,C2与![]() 轴交于A、B两点,其中点A在点B的左侧交y轴于点D.
轴交于A、B两点,其中点A在点B的左侧交y轴于点D.
(1)求A、B两点的坐标;
(2)对于抛物线C2:![]() 2
2![]() 在第三象限部分的一点P,作PF⊥
在第三象限部分的一点P,作PF⊥![]() 轴于F,交AD于点E,若E关于PD的对称点E′恰好落在
轴于F,交AD于点E,若E关于PD的对称点E′恰好落在![]() 轴上,求P点坐标;
轴上,求P点坐标;
(3)在抛物线C1上是否存在一点G,在抛物线C2上是否存在一点Q,使得以A、B、G、Q四点为顶点的四边形是平行四边形?若存在,求出G、Q两点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
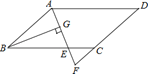
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=![]() ,则△CEF的面积是( )
,则△CEF的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com