练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在正五边形ABCDE中，对角线AD、AC与EB分别相交于点M、N．下列命题：①四边形EDCN是菱形；②四边形MNCD是等腰梯形；③△AEN与△EDM全等；④△AEM与△CBN相似；⑤点M是线段AD、BE、NE的黄金分割点，其中假命题有（     ）

    A．0个        B．1个       C．2个         D．4个

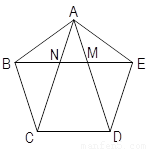
    （第8题图）             

     

    【答案】

    B

    【解析】∵在正五边形ABCDE中，

    ∴AB=BC=CD=DE=AE,BECD,AD BC,AC DE,

    ∴四边形EDCN是菱形, ①正确

    同理四边形BCDM是菱形，

    ∴CN=DE,DM=BN

    ∴CN=DM

    ∴四边形MNCD是等腰梯形, ②正确

    ∴EN=ED=DM=AE=CN=BM=CD

    ∵AN=AC-CN,EM=BE-BM

    ∵BE=AC

    ∴△AEN与△EDM全等, ③正确

    ④△AEM与△CBN相似是错误的

    ⑤点M是线段AD、BE、NE的黄金分割点，正确

    故选B

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    27、问题背景：某课外学习小组在一次学习研讨中，得到了如下两个命题：
    Ⅰ．如图①，在正三角形△ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN．
    Ⅱ．如图②，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．
    任务要求：
    （1）请你从Ⅰ、Ⅱ两个命题中选择一个进行证明．
    （2）如图，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON=108°，请问结论BM=CN是否还成立？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：江西省南昌市2006年初中毕业暨中等学校招生数学试题 题型：059

    问题背景；课外学习小组在一次学习研讨中，得到了如下两个命题：

    ①如图，在正三角形ABC中，M，N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°．则BM＝CN：

    ②如图，在正方形ABCD中，M、N分别是CD、AD上的点．BM与CN相交于点O，若∠BON＝90°．则BM＝CN．

    然后运用类似的思想提出了如下命题：

    ③如图，在正五边形ABCDE中，M、N分别是CD，DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM＝CN．

    任务要求

    (1)请你从①．②，③三个命题中选择一个进行证明；

    (说明：选①做对的得4分，选②做对的得3分，选③做对的得5分)

    (2)请你继续完成下面的探索；

    ①如图，在正n(n≧3)边形ABCDEF…中，M，N分别是CD、DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM＝CN成立(不要求证明)

    ②如图，在正五边形ABCDE中，M、N分别是DE，AE上的点，BM与CN相交于点O，∠BON＝108°时，试问结论BM＝CN是否还成立，若成立，请给予证明．若不成立，请说明理由

    (I)我选________

    证明

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    问题背景：某课外学习小组在一次学习研讨中，得到了如下两个命题：
    Ⅰ．如图①，在正三角形△ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN．
    Ⅱ．如图②，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．
    任务要求：
    （1）请你从Ⅰ、Ⅱ两个命题中选择一个进行证明．
    （2）如图，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON=108°，请问结论BM=CN是否还成立？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2006-2007学年山东省济南市市中区九年级（上）期末数学试卷（解析版） 题型：解答题

    问题背景：某课外学习小组在一次学习研讨中，得到了如下两个命题：
    Ⅰ．如图①，在正三角形△ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN．
    Ⅱ．如图②，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．
    任务要求：
    （1）请你从Ⅰ、Ⅱ两个命题中选择一个进行证明．
    （2）如图，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON=108°，请问结论BM=CN是否还成立？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在正五边形ABCDE内部找一点P，使得四边形ABPE为平行四边形，甲、乙两人的作法如下：

    甲：连接BD、CE，两线段相交于P点，则P即为所求；

    乙：先取CD的中点M，再以A为圆心，AB长为半径画弧，交AM于P点，则P即为所求．
    对于甲、乙两人的作法，下列判断何者正确？（　　）

    A．两人皆正确    B．两人皆错误   C．甲正确，乙错误  D．甲错误，乙正确

    查看答案和解析>>

    同步练习册答案