
【题目】如图表示两辆汽车行驶路程与时间的关系(汽车B在汽车A后出发)的图象,试回答下列问题:

(1)图中l1,l2分别表示哪一辆汽车的路程与时间的关系?
(2)写出汽车A和汽车B行驶的路程s与时间t的函数关系式,并求汽车A和汽车B的速度;
(3)图中交点的实际意义是什么?
【答案】(1)l1表示A车的路程与时间的关系,l2表示B车的路程与时间的关系;(2)汽车B行驶的路程s与时间t的函数关系式y=100t﹣200,汽车B的速度为100km/h.(3)汽车A出发3h(或汽车B出发1h)两车相遇,此时两车行驶路程都是100km.
【解析】
试题分析:(1)分析图形,得知l1表示先出发的那辆,l2表示两小时后出发的那辆,从而得出结论;
(2)设出路程与时间的关系式,分别代入图形中能看出的点,即可得知函数关系式,汽车的速度为函数关系式的斜率;
(3)由y轴表示的路程可知,交点表示两车路程相同,即相遇.
解:(1)∵汽车B在汽车A后出发,
∴l1表示A车的路程与时间的关系,l2表示B车的路程与时间的关系.
(2)设汽车行驶的路程s与时间t的函数关系s=vt+b,
①将(0,0),(3,100)代入,得![]() ,
,
解得v=![]() ,b=0,
,b=0,
∴汽车A行驶的路程s与时间t的函数关系式y=![]() t,汽车A的速度为
t,汽车A的速度为![]() km/h.
km/h.
②将(2,0),(3,100)代入,得![]() ,
,
解得v=100,b=﹣200,
∴汽车B行驶的路程s与时间t的函数关系式y=100t﹣200,汽车B的速度为100km/h.
(3)汽车A出发3h(或汽车B出发1h)两车相遇,此时两车行驶路程都是100km.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).
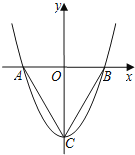
(1)求∠ABC的度数;
(2)若点D是第四象限内抛物线上一点,△ADC的面积为![]() ,求点D的坐标;
,求点D的坐标;
(3)若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C′,点O′,B′均落在此抛物线上,求此时O′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
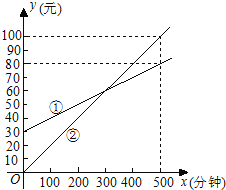
(1)有月租费的收费方式是 (填①或②),月租费是 元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A和B都是5次多项式,则下面说法正确的是()
A. A-B一定是多项式 B. A-B是次数不低于5的整式
C. A+B一定是单项式 D. A+B是次数不高于5的整式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com