
【题目】如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).
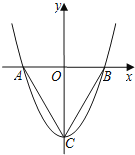
(1)求∠ABC的度数;
(2)若点D是第四象限内抛物线上一点,△ADC的面积为![]() ,求点D的坐标;
,求点D的坐标;
(3)若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C′,点O′,B′均落在此抛物线上,求此时O′的坐标.
【答案】(1)∠ABC=60°;(2)D (![]() ,
,![]() ).(3)O′(﹣
).(3)O′(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)通过求函数解析式,求出相应线段的长度,观察AC=2OA,进而求出∠ABC度数;
(2)通过观察三角形ADC面积与三角形AOC面积相等,可以判断直线OD∥AC,求出直线与抛物线交点即为点D;
(3)利用抛物线解析式设出O′,通过旋转60°,求出点B′的坐标,将点B′代入抛物线解析式即可求出.
解:(1)由题意与y轴交于点C(0,﹣3),
∴得解析式为y=x2﹣3,
令y=0,x=±![]() ,
,
∴B(![]() ,0),A(﹣
,0),A(﹣![]() ,0),
,0),
∴OA=![]() ,OC=3,AC=2
,OC=3,AC=2![]() ,
,
∴∠OCA=30°,
∴∠ABC=60°;
(2)由(1)得:OA=![]() ,OC=3,
,OC=3,
∴S△OAC=![]() ×3×
×3×![]() =
=![]() ,
,
过原点与AC平行的直线y=﹣![]() ,
,
直线与抛物线的交点即为点D,
联立:![]() ,
,
解得x1=![]() ,x2=
,x2=![]() (舍去),
(舍去),
∴D (![]() ,
,![]() ).
).
(3)设点O′(m,m2﹣3),
∵顺时针旋转60°,
则点B′(m+![]() ,m2﹣
,m2﹣![]() ),
),
∴(m+![]() )﹣3=m2﹣
)﹣3=m2﹣![]() ,
,
∴m=﹣![]() ,
,
∴O′(﹣![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】粗心的小红在计算n边形的内角和时,少加了一个内角,求得的内角和是2040°,则这个多边形的边数n和这个内角分别是( )
A.11和60° B.11和120° C.12和60° D.14和120°
查看答案和解析>>
科目:初中数学 来源: 题型:
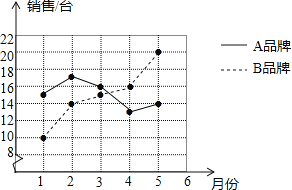
【题目】某商场统计了今年1﹣5月A、B两种品牌冰箱的销售情况,并将获得的数据绘制成如图折线统计图:
(1)根据图中数据填写表格.

(2)通过计算该商场这段时间内A、B两种品牌冰箱月销售量的方差,比较这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).
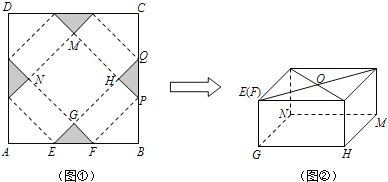
(1)求线段GF的长;(用含x的代数式表示)
(2)当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?
(3)试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示两辆汽车行驶路程与时间的关系(汽车B在汽车A后出发)的图象,试回答下列问题:

(1)图中l1,l2分别表示哪一辆汽车的路程与时间的关系?
(2)写出汽车A和汽车B行驶的路程s与时间t的函数关系式,并求汽车A和汽车B的速度;
(3)图中交点的实际意义是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
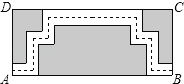
A.100米 B.99米 C.98米 D.74米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
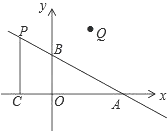
(1)当b=3时,
①求直线AB的解析式;
②若QO=QA,求P点的坐标.
(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com