
ЁОЬтФПЁПШчЭМЂйЃЌABCDЪЧБпГЄЮЊ60cmЕФе§ЗНаЮгВжНЦЌЃЌЧаШЅЫФИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЈвѕгАВПЗжЫљЪОЃЉЃЌЦфжаEЃЌFдкABЩЯЃЛдйбиащЯпелЦ№ЃЌЕуAЃЌBЃЌCЃЌDЧЁКУжиКЯгкЕуOДІЃЈШчЭМЂкЫљЪОЃЉЃЌаЮГЩгавЛИіЕзУцЮЊе§ЗНаЮGHMNЕФАќзАКаЃЌЩшAE=x ЃЈcmЃЉЃЎ
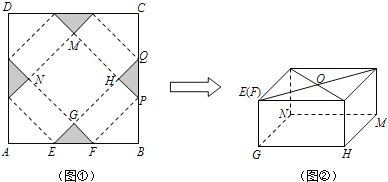
ЃЈ1ЃЉЧѓЯпЖЮGFЕФГЄЃЛЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉЕБxЮЊКЮжЕЪБЃЌОиаЮGHPFЕФУцЛ§S ЃЈcm2ЃЉзюДѓЃПзюДѓУцЛ§ЮЊЖрЩйЃП
ЃЈ3ЃЉЪдЮЪЃКДЫжжАќзАКаФмЗёЗХЯТвЛИіЕзУцАыОЖЮЊ15cmЃЌИпЮЊ10cmЕФдВжљаЮЙЄвеЦЗЃЌЧвЪЙЕУдВжљаЮЙЄвеЦЗЕФвЛИіЕзУцЧЁКУТфдкЭМЂкжаЕФе§ЗНаЮGHMNФкЃПШєФмЃЌЧыЧѓГіТњзуЬѕМўЕФxЕФжЕЛђЗЖЮЇЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ30![]() Љ
Љ![]() xЃЛЃЈ2ЃЉЕБx=15ЪБЃЌSзюДѓ=450ЃЛЃЈ3ЃЉ15
xЃЛЃЈ2ЃЉЕБx=15ЪБЃЌSзюДѓ=450ЃЛЃЈ3ЃЉ15![]() ЁмxЁм30Љ5
ЁмxЁм30Љ5![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉAE=BF=xЃЌОнДЫМДПЩРћгУxБэЪОГіЕШбќжБНЧЁїEFGЕФаББпEFЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЧѓЕУGFЕФГЄЃЛ
ЃЈ2ЃЉЪзЯШРћгУОиаЮЕФУцЛ§ЙЋЪНБэЪОГіУцЛ§SЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓНтЃЛ
ЃЈ3ЃЉЪзЯШЧѓЕУгые§ЗНаЮИїБпЯрЧаЕФЯпЖЮЕФГЄЖШЃЌШЛКѓХаЖЯИпаЁгкЛђЕШгк10cmМДПЩХаЖЯЃЌШЛКѓИљОнNGЕФГЄВЛаЁгк30cmЃЌИпВЛаЁгк10cmМДПЩСаВЛЕШЪНЧѓЕУxЕФЗЖЮЇЃЎ
НтЃКЃЈ1ЃЉЁпAE=BF=xЃЌ
ЁрEF=ABЉAEЉBF=60Љ2xЃЎ
ЁрдкRtЁїGEFжаЃЌGF=![]() EF=
EF=![]() ЁСЃЈ60Љ2xЃЉ=30
ЁСЃЈ60Љ2xЃЉ=30![]() Љ
Љ![]() xЃЛ
xЃЛ
ЃЈ2ЃЉЁпNG=![]() AE=
AE=![]() xЃЌМДGH=NG=
xЃЌМДGH=NG=![]() xЃЌ
xЃЌ
ЁрS=![]() x ЃЈ30
x ЃЈ30![]() Љ
Љ![]() xЃЉ=Љ2x2+60x
xЃЉ=Љ2x2+60x
=Љ2ЃЈxЉ15ЃЉ2+450ЃЛ
ЁпЉ2ЃМ0ЃЌ
ЁрЕБx=15ЪБЃЌSзюДѓ=450ЃЛ
ЃЈ3ЃЉФмЗХЯТЃЎ
РэгЩЪЧЃКЕБдВжљаЮЙЄвеЦЗгыGHMNЯрЧаЪБЃЌx=15![]() ЃЌ
ЃЌ
ДЫЪБЃЌ30![]() Љ
Љ![]() x=30
x=30![]() Љ15
Љ15![]() ЁС
ЁС![]() =30
=30![]() Љ30ЃО10ЃЌЙЪвЛЖЈФмЗХЯТЃЎ
Љ30ЃО10ЃЌЙЪвЛЖЈФмЗХЯТЃЎ
ИљОнЬтвтЕУЃК![]()
НтЕУЃК15![]() ЁмxЁм30Љ5
ЁмxЁм30Љ5![]() ЃЎ
ЃЎ


 ЕМбЇНЬГЬИпжааТПЮБъЯЕСаД№АИ
ЕМбЇНЬГЬИпжааТПЮБъЯЕСаД№АИ аЁбЇПЮЪБЬибЕЯЕСаД№АИ
аЁбЇПЮЪБЬибЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
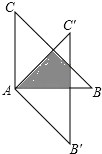
ЁОЬтФПЁПШчЭМЃЌЁїABCШЦЕуAЫГЪБеыа§зЊ45ЁуЕУЕНЁїAЁфBЁфCЁфЃЌШєЁЯBAC=90ЁуЃЌAB=AC=2ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЕШгк ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЧЪа5ФъЧАШЫОљФъЪеШыЮЊnдЊЃЌдЄМЦНёФъШЫОљФъЪеШыЪЧ5ФъЧАЕФ2БЖЖр800дЊЃЌдђНё
ФъШЫОљФъЪеШыНЋДя____ _____дЊ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаМЦЫуе§ШЗЕФЪЧЃЈ ЃЉ
AЃЎx4+x4=2x8 BЃЎx3x2=x6 CЃЎЃЈx2yЃЉ3=x6y3 DЃЎЃЈxЉyЃЉЃЈyЉxЃЉ=x2Љy2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЪЧзјБъдЕуЃЌЖўДЮКЏЪ§y=x2+cЕФЭМЯѓХзЮяЯпНЛxжсгкЕуAЃЌBЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌЉ3ЃЉЃЎ
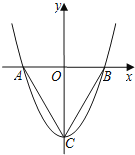
ЃЈ1ЃЉЧѓЁЯABCЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЕуDЪЧЕкЫФЯѓЯоФкХзЮяЯпЩЯвЛЕуЃЌЁїADCЕФУцЛ§ЮЊ![]() ЃЌЧѓЕуDЕФзјБъЃЛ
ЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉШєНЋЁїOBCШЦЦНУцФкФГвЛЕуЫГЪБеыа§зЊ60ЁуЕУЕНЁїOЁфBЁфCЁфЃЌЕуOЁфЃЌBЁфОљТфдкДЫХзЮяЯпЩЯЃЌЧѓДЫЪБOЁфЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЁЭBCЧвBDЃОCDЃЌDFЁЭABЃЌЁїCDEКЭЁїADBЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌИјГіЯТСаНсТлЃЌе§ШЗЕФЪЧ
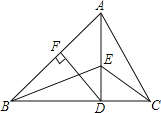
ЂйЁїADCЁеЁїBDEЃЛ
ЂкЁїADFЁеЁїBDFЃЛ
ЂлЁїCDEЁеЁїAFDЃЛ
ЂмЁїACEЁеABEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП
![]()
ЃЈ1ЃЉаДГіAЁЂBСНЕуЫљБэЪОЕФЪ§ЃЌВЂЧѓЯпЖЮABЕФГЄЃЛ
ЃЈ2ЃЉНЋЕуAЯђзѓвЦЖЏ![]() ИіЕЅЮЛГЄЖШЕУЕНЕуCЃЌЕуCБэЪОЕФЪ§ЪЧЖрЩйЃЌВЂдкЪ§жсЩЯБэЪОГіРД
ИіЕЅЮЛГЄЖШЕУЕНЕуCЃЌЕуCБэЪОЕФЪ§ЪЧЖрЩйЃЌВЂдкЪ§жсЩЯБэЪОГіРД
ЃЈ3ЃЉЪ§жсЩЯДцдквЛЕуDЃЌЪЙЕУCЁЂDСНЕуМфЕФОрРыЮЊ8ЃЌЧыаДГіDЕуБэЪОЕФЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЕФШ§ИіЖЅЕуЕФзјБъЮЊЃКAЃЈ2ЃЌ4ЃЉЃЌBЃЈ4ЃЌ3ЃЉЃЌCЃЈ1ЃЌ1ЃЉЃЌжБЯпlЙ§ЕуЃЈЉ1ЃЌ0ЃЉЧвЦНаагкyжсЃЎ
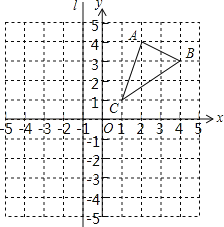
ЃЈ1ЃЉдкЭМжазїГіЁїABCЙигкxжсЖдГЦЕФЁїAЁфBЁфCЁфЃЛ
ЃЈ2ЃЉзїГіЁїABCЙигкжБЯпlЖдГЦЕФЁїA1B1C1ЃЌВЂаДГіЁїA1B1C1Ш§ИіЖЅЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com