
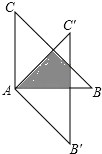
【题目】如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=2,则图中阴影部分的面积等于 .
【答案】2![]() ﹣2.
﹣2.
【解析】
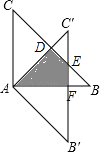
试题分析:AC′与BC交于点D,B′C′与BC交于点E,与AB交于点F,如图,由∠BAC=90°,AB=AC=2可判断△ABC为等腰直角三角形,则∠B=∠C=45°,BC=![]() AB=2
AB=2![]() ,再根据旋转的性质得∠CAC′=45°,AC′=AC=2,∠C=∠C′=45°,则∠ADC=90°,所以AD=
,再根据旋转的性质得∠CAC′=45°,AC′=AC=2,∠C=∠C′=45°,则∠ADC=90°,所以AD=![]() BC=
BC=![]() ,可计算出C′D=AC′﹣AD=2﹣
,可计算出C′D=AC′﹣AD=2﹣![]() ,接着证明△C′DE为等腰直角三角形得到C′D=DE=2﹣
,接着证明△C′DE为等腰直角三角形得到C′D=DE=2﹣![]() ,证明△AC′F为等腰直角三角形得到C′F=AF=
,证明△AC′F为等腰直角三角形得到C′F=AF=![]() AC′=
AC′=![]() ,然后利用图中阴影部分的面积=S△AC′F﹣S△DC′E进行计算即可.
,然后利用图中阴影部分的面积=S△AC′F﹣S△DC′E进行计算即可.
解:AC′与BC交于点D,B′C′与BC交于点E,与AB交于点F,如图,
∵∠BAC=90°,AB=AC=2,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,BC=![]() AB=2
AB=2![]() ,
,
∵△ABC绕点A顺时针旋转45°得到△A′B′C′,
∴∠CAC′=45°,AC′=AC=2,∠C=∠C′=45°,
∴∠ADC=90°,即AD⊥BC,
∴AD=![]() BC=
BC=![]() ,
,
∴C′D=AC′﹣AD=2﹣![]() ,
,
∵△C′DE为等腰直角三角形,
∴C′D=DE=2﹣![]() ,
,
∵∠BAD=90°﹣∠CAC′=45°,
而∠C′=45°,
∴△AC′F为等腰直角三角形,
∴C′F=AF=![]() AC′=
AC′=![]() ,
,
∴图中阴影部分的面积=S△AC′F﹣S△DC′E
=![]() (
(![]() )2﹣
)2﹣![]() (2﹣
(2﹣![]() )2
)2
=2![]() ﹣2.
﹣2.
故答案为2![]() ﹣2.
﹣2.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.
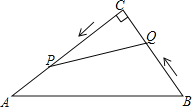
(1)几秒后P、Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1,△ABC的面积为S2,在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )

A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
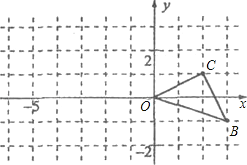
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试通过画图来判定,下列说法正确的是( )
A. 一个直角三角形一定不是等腰三角形 B. 一个等腰三角形一定不是锐角三角形
C. 一个钝角三角形一定不是等腰三角形 D. 一个等边三角形一定不是钝角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:
①(﹣11)+5
②5﹣(﹣![]() )+(﹣7)﹣
)+(﹣7)﹣![]()
③(﹣3)2+(﹣16)÷[(﹣![]() )÷(﹣
)÷(﹣![]() )]
)]
(2)化简并求值
3(x2y+xy2)﹣2(xy+xy2)﹣![]() x2y,其中x是绝对值等于2的负数,y是最大的负整数.
x2y,其中x是绝对值等于2的负数,y是最大的负整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).
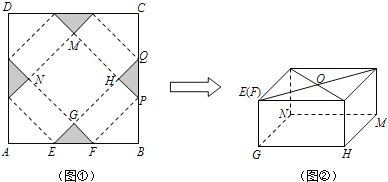
(1)求线段GF的长;(用含x的代数式表示)
(2)当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?
(3)试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com