
【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.

【答案】见解析
【解析】
试题分析:(1)先利用斜边直角边定理证明△OEC和△OFB全等,根据全等三角形对应角相等得到∠B=∠C,再根据等角对等边的性质即可得到AB=AC;
(2)过O作OE⊥AB,OF⊥AC,与(1)的证明思路基本相同.
证明:(1)在Rt△OEC和Rt△OFB中
∵![]() ,
,
∴Rt△OEC≌Rt△OFB(HL),
∴∠B=∠C(全等三角形的对应角相等),
∴AB=AC(等角对等边);
(2)在Rt△OEC和Rt△OFB中,
∵![]() ,
,
∴Rt△OEC≌Rt△OFB(HL),
∴∠OBF=∠OCE,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠FBO+∠OBC=∠OCE+∠OCB,即∠ABC=∠ACB,
∴AB=AC.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,2)是一次函数y=kx+b与反比例函数
),B(﹣1,2)是一次函数y=kx+b与反比例函数![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
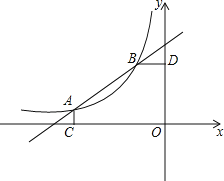
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2﹣x﹣6分解因式.这个式子的常数项﹣6=2×(﹣3),一次项系数﹣1=2+(﹣3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.
(1)分解因式:x2+7x﹣18.
(2)填空:若x2+px﹣8可分解为两个一次因式的积,则整数p的所有可能值是 .
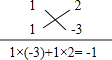
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
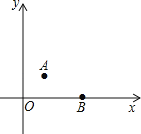
A.(﹣3,1) B.(4,1) C.(﹣2,1) D.(2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 两个关于某直线对称的图形是全等图形;
B. 两个图形全等,它们一定关于某直线对称;
C. 两个全等三角形对应点连线的垂直平分线就是它们的对称轴;
D. 两个三角形关于某直线对称,对称点一定在直线两旁.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
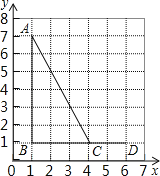
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com