
【题目】如图,BD是等边三角形ABC的角平分线,E是BC延长线上的一点,且CE=CD,DF=BC,垂足为F.BF与EF相等吗?为什么?

【答案】BF与EF相等,证明见解析.
【解析】
根据等边三角形的性质得∠ABC=∠ACB=60°,再由BD是角平分线得∠CBD=30°,接着根据等腰三角形的性质,由CD=CE得到∠CDE=∠E,利用三角形外角性质可计算出∠E=30°,所以∠DBE=∠E,于是可判断△DBE为等腰三角形,然后根据等腰三角形的性质可得BF=EF.
BF与EF相等。理由如下:
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵BD是等边三角形ABC的角平分线,
∴∠CBD=30°,
∵CD=CE,
∴∠CDE=∠E,
而∠BCD=∠CDE+∠E=60°,
∴∠E=30°,
∴∠DBE=∠E,
∴△DBE为等腰三角形,
∵DF⊥BC,
∴BF=EF.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:△NDE≌△MAE;
(2)求证:四边形AMDN是平行四边形;
(3)当AM的值为何值时,四边形AMDN是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D,在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是______。
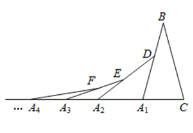
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有【 】

A.1组 B.2组 C.3组 D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC.以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°;⑤DB平分∠ADC.其中正确的结论有( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD中,AB=6,BC=9,沿EF折叠,使点B落在DC边上点P处,点A落在Q处,AD与PQ相交于点H.

(1)如图1,当点P为边DC的中点时,求EC的长;
(2)如图2,当∠CPE=30°,求EC、AF的长;(3)如图2,在(2)条件下,求四边形EPHF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com