
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
【答案】(1)![]() (2)
(2)![]()
【解析】解:(1)在矩形OABC中,
∵B点坐标为(2,3),∴BC边中点D的坐标为(1,3)。
又∵双曲线![]() 的图像经过点D(1,3),
的图像经过点D(1,3),
∴![]() ,∴
,∴![]() 。
。
∴双曲线解析式为![]() 。
。
∵E点在AB上,∴E点的横坐标为2。
又∵![]() 经过点E,∴E点纵坐标为
经过点E,∴E点纵坐标为![]() 。
。
∴E点纵坐标为![]() 。
。
(2)由(1)得,BD=1,BE=![]() ,BC=2,
,BC=2,
∵△FBC∽△DEB,∴![]() ,即
,即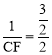 。
。
∴![]() 。∴
。∴![]() ,即点F的坐标为
,即点F的坐标为![]() 。
。
设直线FB的解析式为![]() ,而直线FB经过B,F,,
,而直线FB经过B,F,,
∴ ,解得
,解得![]() 。
。
∴直线FB的解析式为![]() 。
。
(1)根据矩形的性质求出点D的坐标,代入![]() 即可求出k的值,从而由点E在双曲线上,求出点E的坐标。
即可求出k的值,从而由点E在双曲线上,求出点E的坐标。
(2)由△FBC∽△DEB列比例式求出CF的长而得到OF的长,得到点F的坐标,用待定系数法求出直线FB的解析式。


科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
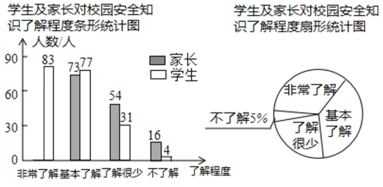
![]() 参与调查的学生及家长共有 人;
参与调查的学生及家长共有 人;
![]() 在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
![]() 在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天昆明市交警大队的一辆警车在东西方向的街上巡视,警车从钟楼A处出发,规定向东方向为正,当天行驶纪录如下(单位:千米)
+10,-9,+7,-15,+6,-5,+4,-2
(1)最后警车是否回到钟楼A处?若没有,在钟楼A处何方,距钟楼A多远?
(2)警车行驶1千米耗油0.2升,油箱有油10升,够不够?若不够,途中还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
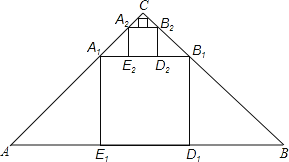
【题目】如图,△ABC是斜边AB的长为3的等腰直角三角形,在△ABC内作第1个内接正方形A1B1D1E1(D1、E1在AB上,A1、B1分别在AC、BC上),再在△A1B1C内接同样的方法作第2个内接正方形A2B2D2E2,…如此下去,操作n次,则第n个小正方形AnBnDnEn 的边长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
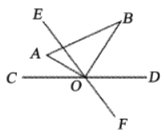
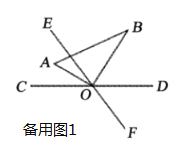
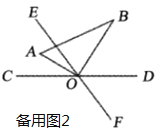
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,将一直角三角尺
,将一直角三角尺![]() 的直角顶点与点
的直角顶点与点![]() 重合,
重合,![]() 平分
平分![]() .
.
(1)![]() 的度数为______________
的度数为______________![]() ;
;
(2)将三角尺![]() 以每秒
以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,同时直线
顺时针旋转,同时直线![]() 也以每秒
也以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,设运动时间为
顺时针旋转,设运动时间为![]() 秒
秒![]() .
.
①求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() ;
;
②求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前某市区的出租车起步价有五种,分别为9元、12元、13元、15元和18元,不同车型的出租车收费标准不同.其中,最为常见的“薄荷绿”出租车的起步价为3公里9元,若超出3公里,3公里外每公里另收1.5元.
(1)如果小明乘“薄荷绿”出租车12公里,那么小明应该支付车费多少元?
(2)如果小丽乘“薄荷绿”出租车的费用为34.5元,那么小丽乘车多少公里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com