
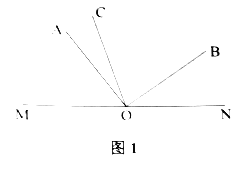
【题目】已知![]() 为直线
为直线![]() 上的一点,且
上的一点,且![]() 为直角,
为直角,![]() 平分
平分![]() .
.
(1)如图1,若![]() ,则
,则![]() 等于多少度;
等于多少度;
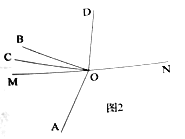
(2)如图2,若![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)∠AOC =18°;(2)∠BON=152°
【解析】
(1)由∠BON=36°,求得∠BOM=144°,由OC平分∠MOB,求得∠COB=72°,由于∠AOB为直角,则由∠AOC=∠AOB-∠COB可求得结论;
(2)设∠BOC=∠MOC=x°,再根据角的关系得出方程,解答后求出结论即可.
解:(1)∵∠BON=36°,
∴∠BOM=144°,
∵OC平分∠MOB,
∴∠COB=72°,
∵∠AOB为直角,
∴∠AOC=∠AOB-∠COB=18°;
(2)设∠BOC=∠MOC=x°,
∵∠AOB为直角,
∴∠AOM=90°-2x°,
∵∠DON-∠AOM=21°,
∴∠DON=∠AOM+21°=111°-2x°,
∵OD平分∠CON,
∴∠CON=222°-4x°,
∵∠CON+∠MOC=180°,
∴222-4x+x=180,
∴x=14,
∴∠BON=180°-∠BOM=180°-28°=152°.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行调查,根据调查结果绘制成如下两幅不完整的统计图.
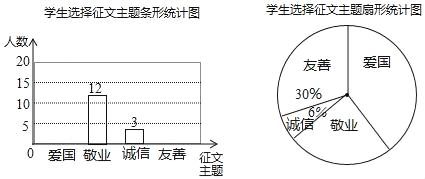
(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,“爱国”主题所对应的圆心角是多少;
(4)如果该校七年级共有![]() 名学生,请估计该校选择以“友善”为主题的七年级学生有多少名.
名学生,请估计该校选择以“友善”为主题的七年级学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
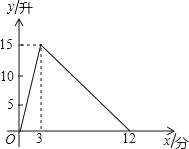
【题目】一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.
①当0≤x≤3时,求y与x之间的函数关系.
②3<x≤12时,求y与x之间的函数关系.
③当容器内的水量大于5升时,求时间x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
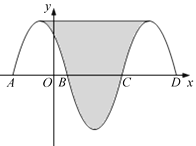
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:∵直线y=3x+7,其中k=3,b=7.
∴点P(﹣1,2)到直线y=3x+7的距离为:
d=![]() =
=![]() =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(﹣1,3)到直线y=x﹣3的距离;
(2)已知⊙Q的圆心Q坐标为(0,3),半径r为3,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=3x+3与y=3x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作思考:如图1,在平面直角坐标系中,等腰直角![]() 的直角顶点
的直角顶点![]() 在原点,将其绕着点
在原点,将其绕着点![]() 旋转,若顶点
旋转,若顶点![]() 恰好落在点
恰好落在点![]() 处.则①
处.则①![]() 的长为______;②点
的长为______;②点![]() 的坐标为______(直接写结果)
的坐标为______(直接写结果)
(2)感悟应用:如图2,在平面直角坐标系中,将等腰直角![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线
,试求直线![]() 的函数表达式.
的函数表达式.
(3)拓展研究:如图3,在直角坐标系中,点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,作
,作![]() 轴,垂足为点
轴,垂足为点![]() 是线段
是线段![]() 上的一个动点,点
上的一个动点,点![]() 是直线
是直线![]() 上一动点.问是否存在以点
上一动点.问是否存在以点![]() 为直角顶点的等腰直角
为直角顶点的等腰直角![]() ,若存在,请直接写出此时
,若存在,请直接写出此时![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
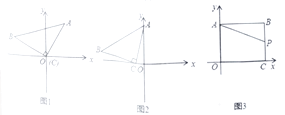
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com