
【题目】如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.
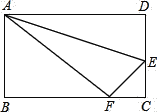
⑴BF= 厘米;
⑵求EC的长.
【答案】(1) 6 ;(2)EC=3 厘米.
【解析】
试题(1)由图形翻折变换的性质可知,AD=AF=10,在Rt△ABF中利用勾股定理即可求解BF的长度;
(2)将CE的长设为x,得出DE=10-x=EF,在Rt△CEF中,根据勾股定理列出方程求解即可.
试题解析:(1)∵△ADE折叠后的图形是△AFE,
∴AD=AF,∠D=∠AFE,DE=EF.
∵AD=BC=10厘米,
∴AF=AD=10厘米.
又∵AB=8厘米,在Rt△ABF中,根据勾股定理,得AB2+BF2=AF2
∴82+BF2=102,
∴BF=6厘米.
(2)设EC=x厘米,则DE=(8-x)厘米, FC=BC-BF=10-6=4厘米.
由题意得EF=DE,FC=4厘米 ,∠C=90°,
由勾股定理得EF2=FC2+EC2
(8-x)2=42+x2
解得:x=3 ,
答:EC长度为3厘米.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
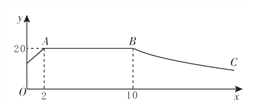
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且大棚内温度为20℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭后大棚内温度y(单位:℃)随光照时间x(单位:h)变化的大致图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
(1)这天恒温系统在保持大棚内温度20℃的时间有 h;
(2)求k的值;
(3)当x=16 h时,大棚内的温度约为多少℃?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为4,点
表示的数为4,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动.设运动的时间为
出发,以每秒2个单位长度的速度向左匀速运动.设运动的时间为![]()
![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点相遇?并写出相遇点所表示的数.
两点相遇?并写出相遇点所表示的数.
(2)当![]() 为何值时,
为何值时,![]() ?
?
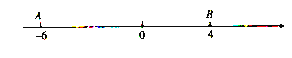
查看答案和解析>>
科目:初中数学 来源: 题型:
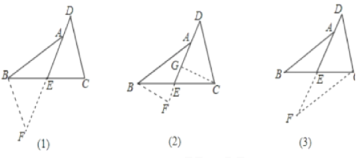
【题目】读下面的题目及分析过程,并按要求进行证明。已知:如图,E是BC的中点,点A在DB上,且
∠BAE=∠CDE,求证:AB=CD
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等。因此,要证明AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形。现给出如下三种添加辅助线的方法,请任意选择其中两种对原题进行证明。
图(1):延长DE到F使得EF=DE
图(2):作CG⊥DE于G,BF⊥DE于F交DE的延长线于F
图(3):过C点作CF∥AB交DE的延长线于F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市有两家出租车公司,收费标准不同,甲公司收费标准为:起步价8元,超过3千米后,超过的部分按照每千米1.5元收费;乙公司收费标准为:起步价11元,超过3千米后,超过的部分按照每千米1.2元收费,车辆行驶![]() 千米,本题中
千米,本题中![]() 取整数,不足1千米的路程按1千米计费,根据上述内容,完成以下问题:
取整数,不足1千米的路程按1千米计费,根据上述内容,完成以下问题:
(1)当![]() 时,乙公司比甲公司贵______元;
时,乙公司比甲公司贵______元;
(2)当![]() ,且
,且![]() 为整数时,甲乙两公司的收费分别是多少?(结果用化简后的含
为整数时,甲乙两公司的收费分别是多少?(结果用化简后的含![]() 的式子表示);
的式子表示);
(3)当行驶路程为18千米时,哪家公司的费用更便宜?便宜多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行调查,根据调查结果绘制成如下两幅不完整的统计图.
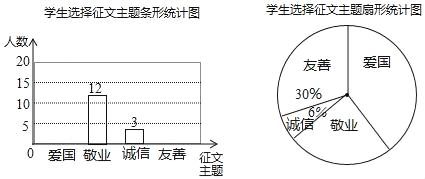
(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,“爱国”主题所对应的圆心角是多少;
(4)如果该校七年级共有![]() 名学生,请估计该校选择以“友善”为主题的七年级学生有多少名.
名学生,请估计该校选择以“友善”为主题的七年级学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:∵直线y=3x+7,其中k=3,b=7.
∴点P(﹣1,2)到直线y=3x+7的距离为:
d=![]() =
=![]() =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(﹣1,3)到直线y=x﹣3的距离;
(2)已知⊙Q的圆心Q坐标为(0,3),半径r为3,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=3x+3与y=3x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com