
ЁОЬтФПЁПФГЪагаСНМвГізтГЕЙЋЫОЃЌЪеЗбБъзМВЛЭЌЃЌМзЙЋЫОЪеЗбБъзМЮЊЃКЦ№ВНМл8дЊЃЌГЌЙ§3ЧЇУзКѓЃЌГЌЙ§ЕФВПЗжАДееУПЧЇУз1.5дЊЪеЗбЃЛввЙЋЫОЪеЗбБъзМЮЊЃКЦ№ВНМл11дЊЃЌГЌЙ§3ЧЇУзКѓЃЌГЌЙ§ЕФВПЗжАДееУПЧЇУз1.2дЊЪеЗбЃЌГЕСОааЪЛ![]() ЧЇУзЃЌБОЬтжа
ЧЇУзЃЌБОЬтжа![]() ШЁећЪ§ЃЌВЛзу1ЧЇУзЕФТЗГЬАД1ЧЇУзМЦЗбЃЌИљОнЩЯЪіФкШнЃЌЭъГЩвдЯТЮЪЬтЃК
ШЁећЪ§ЃЌВЛзу1ЧЇУзЕФТЗГЬАД1ЧЇУзМЦЗбЃЌИљОнЩЯЪіФкШнЃЌЭъГЩвдЯТЮЪЬтЃК
ЃЈ1ЃЉЕБ![]() ЪБЃЌввЙЋЫОБШМзЙЋЫОЙѓ______дЊЃЛ
ЪБЃЌввЙЋЫОБШМзЙЋЫОЙѓ______дЊЃЛ
ЃЈ2ЃЉЕБ![]() ЃЌЧв
ЃЌЧв![]() ЮЊећЪ§ЪБЃЌМзввСНЙЋЫОЕФЪеЗбЗжБ№ЪЧЖрЩйЃПЃЈНсЙћгУЛЏМђКѓЕФКЌ
ЮЊећЪ§ЪБЃЌМзввСНЙЋЫОЕФЪеЗбЗжБ№ЪЧЖрЩйЃПЃЈНсЙћгУЛЏМђКѓЕФКЌ![]() ЕФЪНзгБэЪОЃЉ;
ЕФЪНзгБэЪОЃЉ;
ЃЈ3ЃЉЕБааЪЛТЗГЬЮЊ18ЧЇУзЪБЃЌФФМвЙЋЫОЕФЗбгУИќБувЫЃПБувЫЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ3ЃЛЃЈ2ЃЉМзЙЋЫОЕФЪеЗбЪЧЃК1.5xЃЋ3.5ЃЛввЙЋЫОЕФЪеЗбЪЧЃК1.2xЃЋ7.4ЃЛЃЈ3ЃЉввЙЋЫОЕФЗбгУИќБувЫЃЌБувЫ1.5дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЕБ0ЃМxЃМ3ЪБЃЌМзЙЋЫОЪеЗбЮЊ8дЊЃЌввЙЋЫОЪеЗбЮЊ11дЊЃЌОнДЫПЩЕУД№АИЃЛ
ЃЈ2ЃЉИљОнМзЁЂввСНЙЋЫОЕФЪеЗбБъзМЗжБ№СаГіДњЪ§ЪНМДПЩЃЛ
ЃЈ3ЃЉЕБxЃН18ЪБЃЌЗжБ№ЧѓГіДњЪ§ЪНЕФжЕЃЌБШНЯМДПЩЃЎ
НтЃКЃЈ1ЃЉЕБ0ЃМxЃМ3ЪБЃЌгЩЬтвтЕУЃЌМзЙЋЫОЪеЗбЮЊ8дЊЃЌввЙЋЫОЪеЗбЮЊ11дЊЃЌ
Ёп118ЃН3ЃЈдЊЃЉЃЌ
ЁрввЙЋЫОБШМзЙЋЫОЙѓ3дЊЃЛ
ЃЈ2ЃЉЕБxЃО3ЃЌЧвxЮЊећЪ§ЪБЃЌ
МзЙЋЫОЕФЪеЗбЪЧЃК8ЃЋ1.5ЃЈx3ЃЉЃН1.5xЃЋ3.5ЃЌ
ввЙЋЫОЕФЪеЗбЪЧЃК11ЃЋ1.2ЃЈx3ЃЉЃН1.2xЃЋ7.4ЃЛ
ЃЈ3ЃЉЕБааЪЛТЗГЬЮЊ18ЧЇУзЃЌМДxЃН18ЪБЃЌ
МзЙЋЫОЕФЪеЗбЪЧЃК1.5xЃЋ3.5ЃН1.5ЁС18ЃЋ3.5ЃН30.5ЃЈдЊЃЉЃЌ
ввЙЋЫОЕФЪеЗбЪЧЃК1.2xЃЋ7.4ЃН1.2ЁС18ЃЋ7.4ЃН29ЃЈдЊЃЉЃЌ
Ёп30.529ЃН1.5ЃЈдЊЃЉЃЌ
ЁрввЙЋЫОЕФЗбгУИќБувЫЃЌБувЫ1.5дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
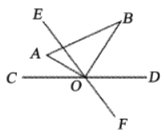
ЁОЬтФПЁПAЁЂBСНГЧЯрОр900ЧЇУзЃЌвЛСОПЭГЕДгAГЧПЊЭљBГЧЃЌГЕЫйЮЊУПаЁЪБ80ЧЇУзЃЌЭЌЪБвЛСОГізтГЕДгBГЧПЊЭљAГЧЃЌГЕЫйЮЊУПаЁЪБ100ЧЇУзЃЌЩшПЭГЕГіЗЂЪБМфЮЊtЃЈаЁЪБЃЉЃЎ
ЬНОПЁЁ ШєПЭГЕЁЂГізтГЕОрAГЧЕФОрРыЗжБ№ЮЊy1ЁЂy2ЃЌаДГіy1ЁЂy2ЙигкtЕФКЏЪ§ЙиЯЕЪНМАздБфСПШЁжЕЗЖЮЇЃЌВЂМЦЫуЕБy1=240ЧЇУзЪБy2ЕФЃЎ
ЗЂЯжЁЁ ЃЈ1ЃЉЩшЕуCЪЧAГЧгыBГЧЕФжаЕуЃЌAC=![]() ABЃЌЭЈЙ§МЦЫуЫЕУїЃКФФИіГЕЯШЕНДяCГЧЃПИУГЕЕНДяCКѓдйОЙ§ЖрЩйаЁЪБЃЌСэвЛИіГЕЛсЕНДяCЃП
ABЃЌЭЈЙ§МЦЫуЫЕУїЃКФФИіГЕЯШЕНДяCГЧЃПИУГЕЕНДяCКѓдйОЙ§ЖрЩйаЁЪБЃЌСэвЛИіГЕЛсЕНДяCЃП
ЃЈ2ЃЉШєСНГЕПлЯрОр100ЧЇУзЪБЃЌЧѓЪБМфtЃЎ
ОіВпЁЁ вбжЊПЭГЕКЭГізтГЕе§КУдкAЃЌBжЎМфЕФЗўЮёеОDДІЯргіЃЌДЫЪБГізтГЕГЫПЭаЁЭѕЭЛШЛНгЕНПЊЛсЭЈжЊЃЌашвЊСЂМДЗЕЛиЃЌДЫЪБаЁЭѕгаСНжжбЁдёЗЕЛиBГЧЕФЗНАИЃК
ЗНАИвЛЃКМЬајГЫзјГізтГЕЕНCГЧЃЌМггЭКѓСЂПЬЗЕЛиBГЧЃЌГізтГЕМггЭЪБМфКіТдВЛМЦЃЛ
ЗНАИЖўЃКдкDДІЛЛГЫПЭГЕЗЕЛиBГЧЃЎ
ЪдЭЈЙ§МЦЫуЃЌЗжЮіаЁЭѕбЁдёФФжжЗНЪНФмИќПьЕНДяBГЧЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌНЋвЛжБНЧШ§НЧГп
ЃЌНЋвЛжБНЧШ§НЧГп![]() ЕФжБНЧЖЅЕугыЕу
ЕФжБНЧЖЅЕугыЕу![]() жиКЯЃЌ
жиКЯЃЌ![]() ЦНЗж
ЦНЗж![]() .
.
ЃЈ1ЃЉ![]() ЕФЖШЪ§ЮЊ______________
ЕФЖШЪ§ЮЊ______________![]() ЃЛ
ЃЛ
ЃЈ2ЃЉНЋШ§НЧГп![]() вдУПУы
вдУПУы![]() ЕФЫйЖШШЦЕу
ЕФЫйЖШШЦЕу![]() ЫГЪБеыа§зЊЃЌЭЌЪБжБЯп
ЫГЪБеыа§зЊЃЌЭЌЪБжБЯп![]() вВвдУПУы
вВвдУПУы![]() ЕФЫйЖШШЦЕу
ЕФЫйЖШШЦЕу![]() ЫГЪБеыа§зЊЃЌЩшдЫЖЏЪБМфЮЊ
ЫГЪБеыа§зЊЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы
Уы![]() .
.
ЂйЧѓЕБ![]() ЮЊКЮжЕЪБЃЌжБЯп
ЮЊКЮжЕЪБЃЌжБЯп![]() ЦНЗж
ЦНЗж![]() ЃЛ
ЃЛ
ЂкЧѓЕБ![]() ЮЊКЮжЕЪБЃЌжБЯп
ЮЊКЮжЕЪБЃЌжБЯп![]() ЦНЗж
ЦНЗж![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+c(aЁй0)ЕФЭМЯѓШчЭМЫљЪОЃЌИјГівдЯТНсТлЃКЂйa+b+cЃМ0ЃЛЂкaЃb+cЃМ0ЃЛЂлb+2aЃМ0ЃЛЂмabcЃО0ЃЌЦфжае§ШЗЕФЪЧ( )
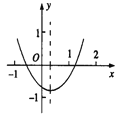
A. ЂйЂкЂл B. ЂкЂл C. ЂлЂм D. ЂйЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌелЕўГЄЗНаЮвЛБпADЃЌЕуDТфдкBCБпЕФЕуFДІЃЌвбжЊBC=10РхУзЃЌAB=8РхУз.
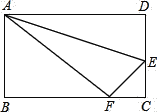
ЂХBF= РхУзЃЛ
ЂЦЧѓECЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъашвЊЙКНјМзЁЂввСНжжЩЬЦЗЙВ160МўЃЌЦфНјМлКЭЪлМлШчЯТБэЃК(зЂЃКЛёРћ=ЪлМлЃНјМл)

(1)ШєЩЬЕъМЦЛЎЯњЪлЭъетХњЩЬЦЗКѓФмЛёРћ1 100дЊЃЌЧыЮЪМзЁЂввСНжжЩЬЦЗгІЗжБ№ЙКНјЖрЩйМўЃП
(2)ШєЩЬЕъМЦЛЎЭЖШызЪН№Щйгк4300дЊЃЌЧвЯњЪлЭъетХњЩЬЦЗКѓЛёРћЖргк1260дЊЃЌЧыЮЪгаФФМИжжЙКЛѕЗНАИЃПВЂжИГіЛёРћзюДѓЕФЙКЛѕЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃН4ЃЌACЃН6ЃЌЁЯABCКЭЁЯACBЕФЦНЗжЯпНЛгкOЕуЃЌЙ§ЕуOзїBCЕФЦНааЯпНЛABгкMЕуЃЌНЛACгкNЕуЃЌдђЁїAMNЕФжмГЄЮЊЃЈ ЃЉ
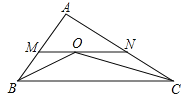
A. 7 B. 8 C. 9 D. 10
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
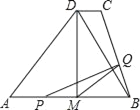
ЁОЬтФПЁПШчЭМЃЌMЮЊЕШбќЁїABDЕФЕзABЕФжаЕуЃЌЙ§DзїDCЁЮABЃЌСЌНсBCЃЛAB=8cmЃЌDM=4cmЃЌDC=1cmЃЌЖЏЕуPздAЕуГіЗЂЃЌдкABЩЯдШЫйдЫЖЏЃЌЖЏЕуQздЕуBГіЗЂЃЌдкелЯпBCЉCDЩЯдШЫйдЫЖЏЃЌЫйЖШОљЮЊ1cm/sЃЌЕБЦфжавЛИіЖЏЕуЕНДяжеЕуЪБЃЌЫќУЧЭЌЪБЭЃжЙдЫЖЏЃЌЩшЕуPдЫЖЏtЃЈsЃЉЪБЃЌЁїMPQЕФУцЛ§ЮЊSЃЈВЛФмЙЙГЩЁїMPQЕФЖЏЕуГ§ЭтЃЉЃЎ
ЃЈ1ЃЉtЃЈsЃЉЮЊКЮжЕЪБЃЌЕуQдкBCЩЯдЫЖЏЃЌtЃЈsЃЉЮЊКЮжЕЪБЃЌЕуQдкCDЩЯдЫЖЏЃЛ
ЃЈ2ЃЉЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБtЮЊКЮжЕЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЪЧЖрЩйЃП
ЃЈ4ЃЉЕБЕуQдкCDЩЯдЫЖЏЪБЃЌжБНгаДГіtЮЊКЮжЕЪБЃЌЁїMPQЪЧЕШбќШ§НЧаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШёНЧЁїABCФкНггкЁбOЃЌШєЁбOЕФАыОЖЮЊ6ЃЌsinA=![]() ЃЌЧѓBCЕФГЄЃЎ
ЃЌЧѓBCЕФГЄЃЎ
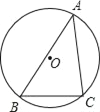
ЁОД№АИЁПBC=8ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЭЈЙ§зїИЈжњЯпЙЙГЩжБНЧШ§НЧаЮЃЌдйРћгУШ§НЧКЏЪ§жЊЪЖНјааЧѓНтЃЎ
ЪдЬтНтЮіЃКзїЁбOЕФжБОЖCDЃЌСЌНгBDЃЌдђCD=2ЁС6=12.
Ёп![]()
Ёр![]()
Ёр![]()
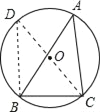
ЕуОІЃКжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧ.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
22
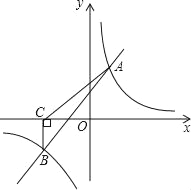
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=k1x+bгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓНЛгкAЃЈ2ЃЌmЃЉЃЌBЃЈnЃЌЉ2ЃЉСНЕуЃЎЙ§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊCЃЌЧвSЁїABC=5ЃЎ
ЕФЭМЯѓНЛгкAЃЈ2ЃЌmЃЉЃЌBЃЈnЃЌЉ2ЃЉСНЕуЃЎЙ§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊCЃЌЧвSЁїABC=5ЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЫљИјЬѕМўЃЌЧыжБНгаДГіВЛЕШЪНk1x+bЃО![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ3ЃЉШєPЃЈpЃЌy1ЃЉЃЌQЃЈЉ2ЃЌy2ЃЉЪЧКЏЪ§y=![]() ЭМЯѓЩЯЕФСНЕуЃЌЧвy1Ёнy2ЃЌЧѓЪЕЪ§pЕФШЁжЕЗЖЮЇЃЎ
ЭМЯѓЩЯЕФСНЕуЃЌЧвy1Ёнy2ЃЌЧѓЪЕЪ§pЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com