练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AB＝4，AC＝6，∠ABC和∠ACB的平分线交于O点，过点O作BC的平行线交AB于M点，交AC于N点，则△AMN的周长为（ ）

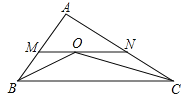
    A. 7 B. 8 C. 9 D. 10

    【答案】D

    【解析】

    利用角平分线及平行线性质，结合等腰三角形的判定得到MB=MO，NC=NO，将三角形AMN周长转化为AB+AC，求出即可．

    ∵BO为∠ABC的平分线，CO为∠ACB的平分线，∴∠ABO=∠CBO，∠ACO=∠BCO．

    ∵MN∥BC，∴∠MOB=∠OBC，∠NOC=∠BCO，∴∠ABO=∠MOB，∠NOC=∠ACO，∴MB=MO，NC=NO，∴MN=MO+NO=MB+NC．

    ∵AB=4，AC=6，∴△AMN周长为AM+MN+AN=AM+MB+AN+NC=AB+AC=10．

    故答案为：10．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了迎接期末考试，某中学对全校七年级学生进行了一次数学摸底考试，并随机抽取了部分学生的测试成绩作为样本进行分析，绘制成了如图两幅不完整的统计图，请根据图中所给出的信息，解答下列问题：

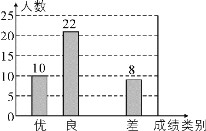
    (1)在这次调查中，被抽取的学生的总人数为多少？

    (2)请将表示成绩类别为“中”的条形统计图补充完整.

    (3)在扇形统计图中，表示成绩类别为“优”的扇形所对应的圆心角的度数是多少？

    (4)学校七年级共有1000人参加了这次数学考试，估计该校七年级共有多少名学生的数学成绩可以达到优秀.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

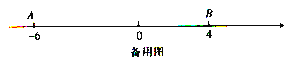
    【题目】如图，数轴上点表示的数为，点表示的数为4，点从点出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点从点出发，以每秒2个单位长度的速度向左匀速运动.设运动的时间为.

    (1)当为何值时，、两点相遇？并写出相遇点所表示的数.

    (2)当为何值时，?

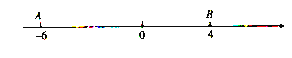
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市有两家出租车公司，收费标准不同，甲公司收费标准为：起步价8元，超过3千米后，超过的部分按照每千米1.5元收费；乙公司收费标准为：起步价11元，超过3千米后，超过的部分按照每千米1.2元收费，车辆行驶千米，本题中取整数，不足1千米的路程按1千米计费，根据上述内容，完成以下问题：

    （1）当时，乙公司比甲公司贵______元；

    （2）当，且为整数时，甲乙两公司的收费分别是多少？（结果用化简后的含的式子表示）;

    （3）当行驶路程为18千米时，哪家公司的费用更便宜？便宜多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校七年级开展征文活动，征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个，七年级每名学生按要求都上交了一份征文，学校为了解选择各种征文主题的学生人数，随机抽取了部分征文进行调查，根据调查结果绘制成如下两幅不完整的统计图.

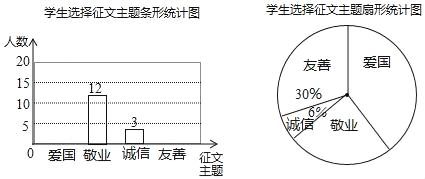
    （1）求共抽取了多少名学生的征文；

    （2）将上面的条形统计图补充完整；

    （3）在扇形统计图中，“爱国”主题所对应的圆心角是多少；

    （4）如果该校七年级共有名学生，请估计该校选择以“友善”为主题的七年级学生有多少名.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场欲招聘一名员工，现有甲、乙两人竞聘．通过计算机、语言和商品知识三项测试，他们各自成绩（百分制）如下表所示：

    应试者

    计算机

    语言

    商品知识

    甲

    70

    50

    80

    乙

    60

    60

    80

    （1）若商场需要招聘负责将商品拆装上架的人员，对计算机、语言和商品知识分别赋权2，3，5，计算两名应试者的平均成绩．从成绩看，应该录取谁？

    （2）若商场需要招聘电脑收银员，计算机、语言和商品知识成绩分别占50%，30%，20%，计算两名应试者的平均成绩．从成绩看，应该录取谁？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场第一次用11000元购进某款拼装机器人进行销售，很快销售一空，商家又用24000元第二次购进同款机器人，所购进数量是第一次的2倍，但单价贵了10元．

    （1）求该商家第一次购进机器人多少个？

    （2）若所有机器人都按相同的标价销售，要求全部销售完毕的利润率不低于20%（不考虑其它因素），那么每个机器人的标价至少是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

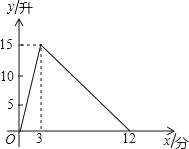
    【题目】一个有进水管与出水管的容器，从某时刻开始的3分内只进水不出水，在随后的9分内既进水又出水，每分的进水量和出水量都是常数．容器内的水量y（单位：升）与时间x（单位：分）之间的关系如图所示．

    ①当0≤x≤3时，求y与x之间的函数关系．

    ②3＜x≤12时，求y与x之间的函数关系．

    ③当容器内的水量大于5升时，求时间x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知数轴上点A表示的数为﹣6，点B在数轴上A点右侧，且AB＝14，动点M从点A出发，以每秒5个单位长度的速度沿数轴向右匀速运动，设运动时间为t（t＞0）秒．

    （1）写出数轴上点B表示的数　 　，点M表示的数　 　（用含t的式子表示）；

    （2）动点N从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点M，N同时出发，问点M运动多少秒时追上点N？

    （3）若P为AM的中点，F为MB的中点，点M在运动过程中，线段PF的长度是否发生变化？若变化，请说明理由；若不变，请求出线段PF的长．

    查看答案和解析>>

    同步练习册答案