

 当CE= 时,
当CE= 时, .
. 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源:不详 题型:解答题
 |  | ||
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 绕点
绕点 旋转后得到
旋转后得到 ,我们称点
,我们称点 和点
和点 、点
、点 和点
和点 、点
、点 和点
和点 分别是对应点,把点
分别是对应点,把点 称为旋转中心。
称为旋转中心。
 顺时针旋转后,线段
顺时针旋转后,线段 的对应线段为线段
的对应线段为线段 ,请你利用圆规、直尺等工具,①作出旋转中心
,请你利用圆规、直尺等工具,①作出旋转中心 ,②作出
,②作出 绕点
绕点 旋转后的
旋转后的 。(要求保留作图痕迹,并说明作法)
。(要求保留作图痕迹,并说明作法)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 ,如图11放置,点
,如图11放置,点 、
、 重合,点
重合,点 在
在 上,
上, 与
与 交于点
交于点 .
. ,
, ,
, .
.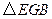 是等腰三角形;
是等腰三角形; 不动,若
不动,若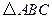 绕点
绕点 逆时针旋转.问首次使四边形
逆时针旋转.问首次使四边形 成为以
成为以 为底的梯形时,(如图12).旋转角α的度数是 度,并请你求出此时梯形的高.
为底的梯形时,(如图12).旋转角α的度数是 度,并请你求出此时梯形的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com