
科目:初中数学 来源:2016届江西省高安市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
阅读材料:如图(一),△ABC的周长为 ,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积

∵ S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB= ,S△OBC=
,S△OBC= ,S△OCA =
,S△OCA =
∴S△ABC= +
+ +
+ =
= (可作为三角形内切圆半径公式)
(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:初中数学 来源:2016届江西省高安市九年级下学期第一次模拟考试数学试卷(解析版) 题型:选择题
已知□ABCD中,对角线AC、BD交于点O,下列式子中一定成立的是 ( )

A.AC⊥BD B.OA=0C C.AC=BD D.A0=OD
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省九年级年级上期末考试数学试卷(解析版) 题型:解答题
如图,正方形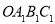 的边长为1,以
的边长为1,以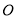 为圆心、
为圆心、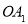 为半径作扇形OA1C1弧A1C1与
为半径作扇形OA1C1弧A1C1与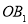 相交于点
相交于点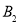 ,设正方形
,设正方形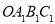 与扇形
与扇形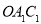 之间的阴影部分的面积为
之间的阴影部分的面积为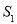 ;然后以
;然后以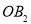 为对角线作正方形
为对角线作正方形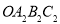 ,又以
,又以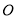 为圆心,、
为圆心,、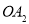 为半径作扇形
为半径作扇形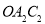 ,弧A2C2与
,弧A2C2与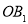 相交于点
相交于点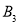 ,设正方形
,设正方形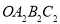 与扇形
与扇形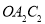 之间的阴影部分面积为
之间的阴影部分面积为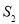 ;按此规律继续作下去,设正方形
;按此规律继续作下去,设正方形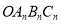 与扇形
与扇形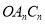 之间的阴影部分面积为
之间的阴影部分面积为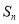 .
.

(1)求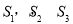 ;
;
(2)写出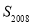 ;
;
(3)试猜想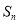 (用含
(用含 的代数式表示,
的代数式表示,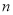 为正整数).
为正整数).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省九年级年级上期末考试数学试卷(解析版) 题型:填空题
端午节吃粽子是中华民族的习惯.今年农历五月初五早餐时,小明妈妈端上一盘粽子,其中有3个肉馅粽子和7个豆沙馅粽子,小明从中任意拿出一个,恰好拿到肉馅粽子的概率是_____.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省九年级年级上期末考试数学试卷(解析版) 题型:选择题
在平面直角坐标系中,点A(2,3)与点B关于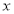 轴对称,则点B的坐标为
轴对称,则点B的坐标为
A.(3,2) B.(-2,-3) C.(-2,3) D.(2,-3)
查看答案和解析>>
科目:初中数学 来源:2016届安徽省芜湖市南陵县九年级下学期中考第一次模拟考试数学试卷(解析版) 题型:填空题
一个暗箱里放有a个除颜色外完全相同的球,这a个球中红球只有3个.若每次将球搅匀后,任意摸出1个球记下颜色再放回暗箱.通过大量重复摸球试验后发现,摸到红球的频率稳定在20%附近,那么可以推算出a的值大约是 .
查看答案和解析>>
科目:初中数学 来源:2016届江苏省无锡市九年级3月阶段测试数学试卷(解析版) 题型:解答题
某中学公司组织初三505名学生外出社会综合实践活动,现打算租用A、B 两种型号的汽车,并且每辆车上都安排1名导游,如果租用这两种型号的汽车各5辆,则刚好坐满;如果全部租用B型汽车,则需13辆汽车,且其中一辆会有2个空位,其余汽车都坐满.(注:同种型号的汽车乘客座位数相同)
(1)A、B两种型号的汽车分别有多少个乘客座位?
(2)综合考虑多种因素,最后该公司决定租用9辆汽车,问最多安排几辆B型汽车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com