
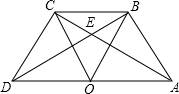
 如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小.
如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小.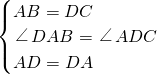 ,
,


科目:初中数学 来源: 题型:
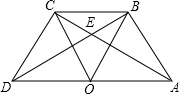
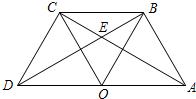 22、如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小.
22、如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小.查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市西城区(北区)八年级上学期期末考试数学试卷(带解析) 题型:解答题
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,且MB=MG.试探究ND,DG与AD数量之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市西城区(北区)八年级上学期期末考试数学试卷(解析版) 题型:解答题
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.
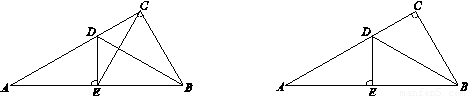
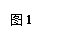
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,且MB=MG.试探究ND,DG与AD数量之间的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com