
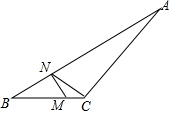
 如图,在△ABC中,∠B=30°,M为BC上一点且MC:MB=m:n,MN⊥AB于N,联结CN,则cot∠CNA的值为$\frac{\sqrt{3}m}{m+n}$.
如图,在△ABC中,∠B=30°,M为BC上一点且MC:MB=m:n,MN⊥AB于N,联结CN,则cot∠CNA的值为$\frac{\sqrt{3}m}{m+n}$. 分析 过点C作CG⊥AB于点G,设MC=m,MB=n,根据∠B=30°分别求出BN、BG的长度,然后求出$\frac{NG}{CG}$的值即可.
解答 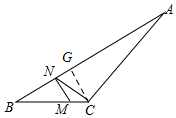 解:过点C作CG⊥AB于点G,
解:过点C作CG⊥AB于点G,
设MC=m,MB=n,
∵∠B=30°,
∴MN=$\frac{n}{2}$,
由勾股定理可知:BN=$\frac{\sqrt{3}n}{2}$,
∵BC=m+n,
∴CG=$\frac{m+n}{2}$,
∴由勾股定理定理:BG=$\frac{\sqrt{3}m+\sqrt{3}n}{2}$,
∴NG=BG-BN=$\frac{\sqrt{3}m}{2}$,
∴cot∠CNA=$\frac{NG}{CG}$=$\frac{\sqrt{3}m}{m+n}$
点评 本题考查解直角三角形,涉及勾股定理,锐角三角函数,直角三角形的性质.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
 如图在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
如图在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
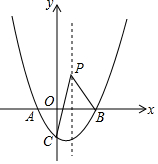 已知抛物线y=x2-2x-3与x轴交于点A、B,与y轴交于点C,P是抛物线对称轴上的一个动点,则当|PB-PC|达到最大值时,点P的坐标为(1,-6).
已知抛物线y=x2-2x-3与x轴交于点A、B,与y轴交于点C,P是抛物线对称轴上的一个动点,则当|PB-PC|达到最大值时,点P的坐标为(1,-6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ③④ | B. | .②④ | C. | ①④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
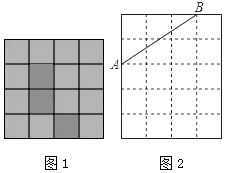 (1)如图1是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形 (涂一个即可);
(1)如图1是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形 (涂一个即可);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
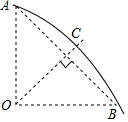 如图,一条公路的转弯处是一段圆弧(图中的AB弧),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D,AB=12m,CD=2m.求这段弯路的半径.
如图,一条公路的转弯处是一段圆弧(图中的AB弧),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D,AB=12m,CD=2m.求这段弯路的半径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com