已知关于x的方程(m-1)x2-2mx+m=0有两个不相等的实数根x1、x2;
(1)求m的取值范围;
(2)若(x1-x2)2=8,求m的值.
解:(1)∵a=m-1,b=-2m,c=m,
而方程有两个不相等的实数根,
∴△=b
2-4ac=4m
2-4(m-1)m=4m>0,
∴m>0(m≠1);
(2)∵
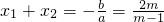
,
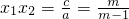
,
∴(x
1-x
2)
2=(x
1+x
2)
2-4x
1x
2=
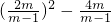
=8,
解得:m
1=2,m
2=

.
经检验2和

都是方程的解.
分析:(1)根据一元二次方程的根的判别式△>0时,方程有两个不相等的实数根,建立关于m的不等式,然后求出m的取值范围;
(2)把根与系数的关系式代入(x
1-x
2)
2=8即(x
1-x
2)
2=(x
1+x
2)
2-4x
1x
2=8,代入即可得到一个关于m的方程,求得m的值.
点评:总结:1、一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根
(3)△<0?方程没有实数根.
2、若一元二次方程有实根,则根与系数的关系为:x
1+x
2=

,x
1•x
2=

.

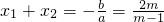 ,
,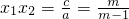 ,
,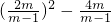 =8,
=8, .
. 都是方程的解.
都是方程的解. ,x1•x2=
,x1•x2= .
. 
