练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，F是平行四边形ABCD对角线BD上的点，BF：FD=1：3，则BE：EC=（　　）

    　 A．  B．  C．  D．


    A

    考点： 相似三角形的判定与性质；平行四边形的性质． 

    分析： 由平行四边形的性质易证两三角形相似，根据相似三角形的性质可解．

    解答： 解：∵ABCD是平行四边形

    ∴AD∥BC

    ∴△BFE∽△DFA

    ∴BE：AD=BF：FD=1：3

    ∴BE：EC=BE：（BC﹣BE）=BE：（AD﹣BE）=1：（3﹣1）

    ∴BE：EC=1：2

    故选A．

    点评： 本题考查了相似三角形的性质；其中由相似三角形的性质得出比例式是解题关键．注意：求相似比不仅要认准对应边，还需注意两个三角形的先后次序．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若|a|=5，|b|=1，且a﹣b＜0，则a+b的值等于（　　）

    　 A． 4或6 B． 4或﹣6 C． ﹣6或6 D． ﹣6或﹣4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    根据反比例函数y=﹣的图象（请画图）回答问题：当函数值为正时，x的取值范围是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若x：y=1：2，则=　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，P为AB上一点，在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足△APC与△ACB相似的条件是　（只填序号）．

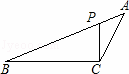
    查看答案和解析>>

    科目：初中数学 来源： 题型：


     

     +|7|+（）0+（）﹣1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某工厂生产的某种产品按质量分为10个档次．第1档次（最低档次）的产品一天能生产76件，每件利润10元．每提高一个档次，每件利润增加2元，但一天产量减少4件．若生产第x档次的产品一天的总利润为1080元，求该产品的质量档次．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点D在△ABC的边AC上，要判定△ADB与△ABC相似，添加一个条件，不正确的是（　　）

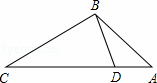
    　 A． ∠ABD=∠C B． ∠ADB=∠ABC C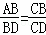．  D．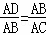

    查看答案和解析>>

    科目：初中数学 来源： 题型：


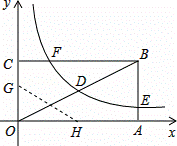
    如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数y=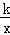（k≠0）在第一象限内的图象经过点D、E，且D点的横坐标是它的纵坐标的2倍．

    （1）求边AB的长；

    （2）求反比例函数的解析式和n的值；

    （3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．

    查看答案和解析>>

    同步练习册答案