
 在△ABC中,总有$\frac{AB}{sinC}$=$\frac{AC}{sinB}$=$\frac{BC}{sinA}$,利用这个知识请解答下题:
在△ABC中,总有$\frac{AB}{sinC}$=$\frac{AC}{sinB}$=$\frac{BC}{sinA}$,利用这个知识请解答下题:分析 (1)在△AEC中,利用正弦定理求得sinC,然后在△ABC中利用正弦定理求得AB的长;
(2)在△ABE中利用余弦定理即可求得BE的长,然后利用速度公式求解.
解答 解:(1)轮船从C处到点B用了80分钟,从点B处到点E用了20分钟,轮船保持匀速直线运动,
设BC=4EB,设BE=x,BC=4x,
在△AEC中,由正弦定理得:
sinC=$\frac{AE•sin∠EAC}{EC}$=$\frac{5sin150°}{5x}$=$\frac{1}{2x}$,
在△ABC中,由正弦定理得,
AB=$\frac{BC•sinC}{sin120°}$=$\frac{4x-\frac{1}{2x}}{sin120°}$=$\frac{4}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$;
(2)在△ABE中,由余弦定理得 BE2=AB2+AE2-2AB•AE•cos30°,
∴BE2=25+$\frac{16}{3}$-2×5×$\frac{4\sqrt{3}}{3}×\frac{\sqrt{3}}{2}$=$\frac{31}{3}$,
∴BE=$\sqrt{\frac{31}{3}}$,
∴轮船船速是$\sqrt{\frac{31}{3}}$÷$\frac{20}{60}$=$\sqrt{93}$(千米/时).
点评 本题考查了解直角三角形的应用,正确理解正弦定理和余弦定理的内容是关键.


科目:初中数学 来源: 题型:解答题
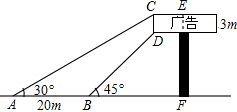 如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号).
如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
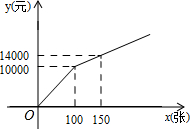 在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com