
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=a��x��2��2��4��y�ύ�ڵ�A������ΪB����A������Ϊ��0����2������C���������ϣ������A��B�غϣ�������C��y��Ĵ��߽��������ڵ�D������AC��AD��CD�����C�ĺ�����Ϊm��
��1������������������Ӧ�ĺ�������ʽ��
��2���ú�m�Ĵ���ʽ��ʾ�߶�CD�ij���
��3����E�������߶Գ�����һ�㣬�ҵ�E��������ȵ�C��������С1������BD��DE������ACD�����ΪS1����BDE�����ΪS2����S1S2��0����S2=![]() S1ʱm��ֵ��
S1ʱm��ֵ��
��4����������y=a��x��2��2��4��x=2ƽ�ƣ��õ�������y=a��x��2��2+k������C��y��ƽ������������y=a��x��2��2+k���ڵ�F����CD��y�ύ�ڵ�G����CD=6��ֱ��д��ʹAC=FG�ĵ�F�����꣮
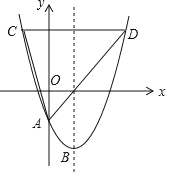
���𰸡���1��y=![]() x2��2x��2����2����m��2����m��0ʱ��CD=4��2m����m��2ʱ��CD=2m��4����3��m=2��
x2��2x��2����2����m��2����m��0ʱ��CD=4��2m����m��2ʱ��CD=2m��4����3��m=2��![]() ��m=
��m=![]() ����4����F����������1����2����1��3����5����2����5��3��
����4����F����������1����2����1��3����5����2����5��3��
�������������������1����A��0��-2����������������a=![]() ���ɣ�
���ɣ�
��2�������ߵĶԳ���Ϊֱ��x=2���ҵ�C�ĺ�����Ϊm���ó���m<2����m��0ʱ��CD=4-2m����m>2ʱ��CD=2m-4��
��3�����BE=![]() m2-2m+1��BE=-
m2-2m+1��BE=-![]() m2+2m-1���������������ϵ�ó����̣��ⷽ�̼��ɣ�
m2+2m-1���������������ϵ�ó����̣��ⷽ�̼��ɣ�
��4��������ó����ı���AGCF�Ǿ��Σ������C�����꣬��������ۣ����ݵ�������ϵ���ɵó��𰸣�
�����������1����������y=a��x��2��2��4��y�ύ�ڵ�A��0����2����
����2=4a��4��
��ã�a=![]() ��
��
����������������Ӧ�ĺ�������ʽΪy=![]() ��x��2��2��4��
��x��2��2��4��
��y=![]() x2��2x��2��
x2��2x��2��
��2����������y=![]() ��x��2��2��4�ĶԳ���Ϊֱ��x=2���ҵ�C�ĺ�����Ϊm��
��x��2��2��4�ĶԳ���Ϊֱ��x=2���ҵ�C�ĺ�����Ϊm��
�൱m��2����m��0ʱ��CD=4��2m��
��m��2ʱ��CD=2m��4��
��3����B��2����4����E��2�� ![]() m2��2m��3����
m2��2m��3����
��BE=![]() m2��2m+1��BE=��
m2��2m+1��BE=��![]() m2+2m��1��
m2+2m��1��
��S1=![]() CD��
CD��![]() m2��2m����S1=
m2��2m����S1=![]() CD����
CD����![]()
![]() CD��
CD��![]() m2��2m+1����S2=
m2��2m+1����S2=![]() CD����
CD����![]() m2+2m��1����
m2+2m��1����
��S2=![]() S1��
S1��
��4��![]() m2��2m��=3��
m2��2m��=3��![]() m2��2m+1������4��
m2��2m+1������4��![]() m2��2m��=��3��
m2��2m��=��3��![]() m2��2m+1����
m2��2m+1����
��ã�m=2��![]() ��=
��=![]() ��
��
��4����AC=FG������AF�����ı���AGCF�Ǿ��Σ�
��CD=6�������ߵĶԳ���Ϊx=2��
���C�ĺ�����Ϊ��1��5��
�ٵ���C�ĺ�����Ϊ��1ʱ����C��������=![]() ������1��2��2������1����2=
������1��2��2������1����2=![]() ��
��
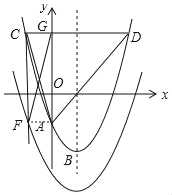
������������ƽ��ʱ����ͼ��ʾ��
�ߵ�A������Ϊ��0����2����
���F����������1����2����
������������ƽ��ʱ��ͬ���ó���F������Ϊ����1��3����
�ڵ���C�ĺ�����Ϊ5ʱ����C��������Ϊ![]() ��
��
������������ƽ��ʱ��ͬ���ĵ�F������Ϊ��5����2����
������������ƽ��ʱ��ͬ���ó���F������Ϊ��5��3����
������������F����������1����2����1��3����5����2����5��3����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�1��![]() �У�
��![]() 40����
40����![]() ����
����![]() ��ȡһ��
��ȡһ��![]() ���ӳ�
���ӳ�![]() ��
��![]() ��ʹ���ڵ�2��
��ʹ���ڵ�2��![]() �У�
��![]() ����
����![]() ��ȡһ��
��ȡһ��![]() ���ӳ�
���ӳ�![]() ��
��![]() ��ʹ���ڵ�3��
��ʹ���ڵ�3��![]() �У�
�У�![]() ��������������������ȥ����3������������
��������������������ȥ����3������������![]() Ϊ������ڽǵĶ���Ϊ_____�� ��
Ϊ������ڽǵĶ���Ϊ_____�� ��![]() ������������
������������![]() Ϊ������ڽǵĶ���Ϊ_____�ȣ�
Ϊ������ڽǵĶ���Ϊ_____�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD �У��Ե� A ΪԲ�ģ�AB ��Ϊ�뾶������ AD �ڵ� F���ٷֱ��Ե� B��F ΪԲ�ģ�����![]() BF ����ͬ��Ϊ�뾶�������������ڵ� P������ AP ���ӳ��� BC �ڵ� E������ EF��
BF ����ͬ��Ϊ�뾶�������������ڵ� P������ AP ���ӳ��� BC �ڵ� E������ EF��
��1���������ϳ߹���ͼ�Ĺ��̣�֤���ı��� ABEF �����Σ�
��2�������� ABEF �ı߳�Ϊ 2��AE�� 2 ![]() �������� ABEF �������
�������� ABEF �������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˾����ʦ��ij������Ӫ��ȫ���ڶ�����ij���·�Ͻ��еģ������Ϊ��������Ϊ���������������г���̣���λ��km�����£�
![]() .
.
��.���һ���˿��͵�Ŀ�ĵأ�����ڶ��滹�����棿�ڶ���ǧ�״���
��.�������ʦ����һ�£�����������һ����ʻ�˶�����̣�
��.��ÿǧ����0.1L��������������ʦ��һ�����˶������ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ��![]() �У�
�У�![]() ��D���߶�
��D���߶�![]() ��һ�㣨
��һ�㣨![]() ��������
��������![]() ������C��
������C��![]() �Ĵ��ߣ���
�Ĵ��ߣ���![]() ���ӳ����ڵ�E����
���ӳ����ڵ�E����![]() ���ӳ����ڵ�F.
���ӳ����ڵ�F.
��1�������ⲹȫͼ�Σ�
��2����![]() ����
����![]() �Ĵ�С���ú�
�Ĵ�С���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��3������G���߶�![]() �ϣ�
�ϣ�![]() ������
������![]() .
.
���ж�![]() ��
��![]() ��λ�ù�ϵ��֤����
��λ�ù�ϵ��֤����
���õ�ʽ��ʾ![]() ֮���������ϵ.
֮���������ϵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
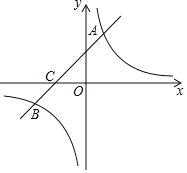
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ཻ�ڵ�һ���������ڵ�
��ͼ���ཻ�ڵ�һ���������ڵ�![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
����÷�����������һ�κ����Ľ���ʽ��
����![]() ������һ��
������һ��![]() ʹ
ʹ![]() �����
�����![]() �����ֵ����
�����ֵ����![]() �����ꣻ
�����ꣻ
��ֱ��д����![]() ʱ��
ʱ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���⣺��������ƽ���������壬��![]() ����(2x��y)2��9������2x��y��3����(��һ��)
����(2x��y)2��9������2x��y��3����(��һ��)
���������������壬��![]() ����x��2y����3����(�ڶ���)
����x��2y����3����(�ڶ���)
���x��3��y��3��
��x��y��ֵ�����ʽ�У���![]() ��(������)
��(������)
�����������������һ����___________����������___________����һ���Dz�___________��������___________����д����ȷ�Ľ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������x��ֵ��
��1��4x2��81=0�� ��2��64��x+1��3=27��
��3����(x��3)3��27 ��4��9(3x��2)2��64��0��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com