
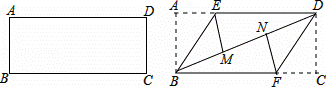
准备一张矩形纸片,按如图操作:
将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
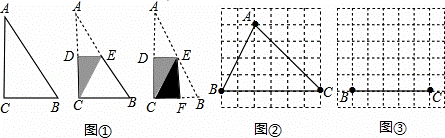
如图①,将一张直角三角形纸片△ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)若一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
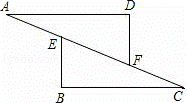
如图,在△ADF与△CBE中,点A,E,F,C在同一直线上,现给出下列四个论断:①AE=CF;②AD=CB;③∠B=∠D;④AD∥BC.请你选择其中三个作为条件,余下的一个作为结论,构成一个命题.请问:
(1)在所有构成的命题中有假命题吗?若有,请写出它的条件和结论(用序号表示);若没有,请说明理由;
(2)在所有构成的真命题中,任意选择一个加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩/分 80 85 90 95
人数/人 1 2 5 2
则这组数据的中位数和平均数分别为( )
A. 90,90 B.90,89 C.85,89 D. 85,90
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com