练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，?ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=4，则CD的长为8．

    分析 因为四边形ABCD是平行四边形，所以OA=OC；再根据点E是BC的中点，得出OE是△ABC的中位线，由OE=4，即可求得AB=CD=8．

    解答 解：∵四边形ABCD是平行四边形，
    ∴OA=OC；
    又∵点E是BC的中点，
    ∴OE是△ABC的中位线，
    则根据三角形的中位线定理可得：AB=CD=2OE=2×4=8．
    故答案为：8．

    点评 此题考查了平行四边形的性质：平行四边形的对角线互相平分．还考查了三角形中位线的性质：三角形的中位线平行且等于三角形第三边的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．如图，Rt△ABC中，∠BAC=90°，AB=AC=2，BC=2$\sqrt{2}$，点D从B点开始运动到C点结束，DE交AC于E，∠ADE=45°，当△ADE是等腰三角形时，AE的长度为1或4-2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

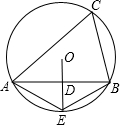    6．如图，△ABC内接于⊙O，D为线段AB的中点，延长OD交⊙O于点E，连接AE，BE，则下列五个结论：①AB⊥DE，②AE=BE，③OD=DE，④∠AEO=∠C，⑤弧AE=弧BE，正确结论的个数是（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，钝角三角形ABC的面积为18，最长边AB=12，BD平分∠ABC，点M、N分别是BD、BC上的动点，则CM+MN的最小值为3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如果⊙A的半径是4cm，⊙B的半径是6cm，圆心距AB=8cm，那么这两个圆的位置关系是相交．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．已知小明家四月份的总支出共计1200元，各项支出如图所示，那么其中用于教育上的支出是180元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

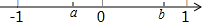    7．实数a、b在数轴上的对应点如图所示，化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{（a-b）^{2}}$的结果是-ab+b-a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知：如图，AE=CF，DE⊥AC，BF⊥AC，垂足分别为E，F，DE=BF．求证：AB∥CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

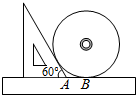    5．如图，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB=3cm，则此光盘的半径是3$\sqrt{3}$cm．

    查看答案和解析>>

    同步练习册答案