Question

5．如图，Rt△ABC中，∠BAC=90°，AB=AC=2，BC=2$\sqrt{2}$，点D从B点开始运动到C点结束，DE交AC于E，∠ADE=45°，当△ADE是等腰三角形时，AE的长度为1或4-2$\sqrt{2}$．

Answer 1

分析 分类讨论：当EA=ED，△ADE为等腰三角形，由∠ADE=45°得到∠EAD=45°，∠AED=90°，则AD平分∠BAC，AD⊥BC，DE⊥AC，然后根据等腰直角三角形的性质得到DE=$\frac{1}{2}$AC=1；当DA=DE，△ADE为等腰三角形，由∠ADE=45°得到∠ADB+∠EDC=180°-45°=135°，而∠EDC+∠DEC=135°，所以∠ADB=∠DEC，根据三角形相似的判定得到△ABD∽△DCE，则BD：CE=AB：DC=AD：DE，利用AD=DE得到AB=DC=2，BD=CE；由于∠BAC=90°，AB=AC=2，根据等腰直角三角形的性质得BC=2$\sqrt{2}$，所以BD=2$\sqrt{2}$-2=EC，然后根据AE=AC-EC进行计算．

解答 解：当EA=ED，△ADE为等腰三角形
∵∠ADE=45°，
∴∠EAD=45°，∠AED=90°，
∵∠BAC=90°，
∴AD平分∠BAC，AD⊥BC，DE⊥AC，如图1，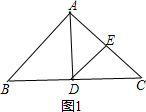
∵AB=AC=2，
∴DE=$\frac{1}{2}$AC=1；
当DA=DE，△ADE为等腰三角形，如图2
∵∠ADE=45°，
∴∠ADB+∠EDC=180°-45°=135°，
而∠EDC+∠DEC=135°，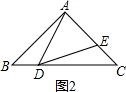
∴∠ADB=∠DEC，
而∠B=∠C，
∴△ABD∽△DCE，
∴BD：CE=AB：DC=AD：DE，
而AD=DE，
∴AB=DC=2，BD=CE，
∵BC=2$\sqrt{2}$，
∴BD=2$\sqrt{2}$-2=EC，
∴AE=AC-EC=2-（2$\sqrt{2}$-2）=4-2$\sqrt{2}$．
故答案为1或4-2$\sqrt{2}$．

点评 本题考查了相似三角形的判定与性质：有两组角对应相等的两个三角形相似；相似三角形的对应线段的比等于相似比．也考查了等腰直角三角形的性质．