
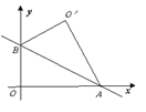
【题目】如图,直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于
轴分别交于![]() 两点,把
两点,把![]() 沿着直线
沿着直线![]() 翻折后得到
翻折后得到![]() ,则点
,则点![]() 的坐标是 ___________ 。
的坐标是 ___________ 。
【答案】(![]() ,3)
,3)
【解析】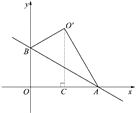
如图,过点O'作O'C⊥OA,垂足为C.
∵点A是直线与x轴的交点,
又∵当y=0时, ![]() ,
,
∴![]() ,
,
∴点A的坐标为(![]() , 0),
, 0),
∴OA=![]() .
.
∵点B是直线与y轴的交点,
又∵当x=0时, ![]() ,
,
∴点B的坐标为(0, 2),
∴OB=2.
∴在Rt△AOB中, ![]() .
.
∵在Rt△AOB中,AB=4,OB=2,即![]() ,
,
∴∠OAB=30°.
∵△AOB沿直线AB翻折得到△AO'B,
∴△AOB≌△AO'B,
∴∠O'AB=∠OAB=30°,O'A=OA=![]() .
.
∴∠OAO'=∠OAB+∠O'AB=60°,即∠CAO'=60°,
∴在Rt△O'CA中,∠AO'C=90°-∠CAO'=90°-60°=30°,
∴在Rt△O'CA中, ![]() ,
, ![]() ,
,
∴OC=OA-AC=![]() -
-![]() =
=![]() .
.
∵OC=![]() ,O'C=3,
,O'C=3,
∴点O'的坐标为(![]() , 3).
, 3).
故本题应填写:(![]() , 3).
, 3).


科目:初中数学 来源: 题型:
【题目】如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】辽宁男篮夺冠后,从4月21日至24日各类媒体关于“辽篮CBA夺冠”的相关文章达到81000篇,将数据81000用科学记数法表示为( )
A. 0.81×104B. 0.81×105C. 8.1×104D. 8.1×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() +bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
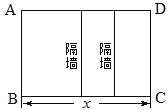
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com