
科目:初中数学 来源: 题型:解答题
| 消费金额a(元)的范围 | 100≤a≤400 | 400≤a≤600 | 600≤a≤800 |
| 获得奖券金额(元) | 40 | 100 | 130 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了美化环境,某学校在教学楼前铺设小广场地面,其图案如图所示,正方形小广场地面的边长是40米.中心建一个直径为正方形边长一半的圆形花坛,四个角各留一个边长为正方形小广场的四分之一的小正方形花坛,种植高大的树木.图中阴影郁分铺设广场砖.
为了美化环境,某学校在教学楼前铺设小广场地面,其图案如图所示,正方形小广场地面的边长是40米.中心建一个直径为正方形边长一半的圆形花坛,四个角各留一个边长为正方形小广场的四分之一的小正方形花坛,种植高大的树木.图中阴影郁分铺设广场砖.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
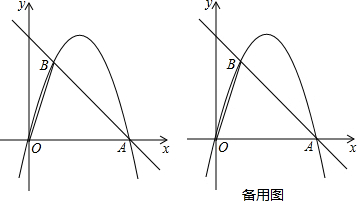
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com