【题目】如图，正方形的边长为，点从开始沿折线以的速度移动，点从开始沿边以的速度移动，如果点，分别从，同时出发，当其中一点到达时，另一点也随之停止运动．

（1）设的面积为，为运动时间，写出关于的函数表达式；

（2）为何值时，的面积为正方形面积的？

【答案】（1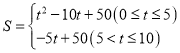）；（2）当t＝5s时，的面积为正方形面积的．

【解析】

（1）当0≤t≤5时，点P在AD上，则△PQB的面积等于正方形的面积减去三个直角三角形的面积；当5＜t≤10时，点P在CD上，△PQB面积等于PQ×10；

（2）结合（1）中的结论，分别列出方程求解即可．

解：（1）当0≤t≤5时，点P在AD上，

由题意得：AP＝2t，DP＝10－2t，DQ＝t，CQ＝10－t，

∵S△PQB＝S正方形ABCD－S△APB－S△DPQ－S△BCQ，

∴；

当5＜t≤10时，点P在CD上，

由题意得：PQ＝t－（2t－10）＝10－t，

∴，

综上所述：；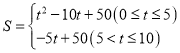

（2）S正方形ABCD＝10×10＝100，

当0≤t≤5时，由题意得：，

解得：t＝5；

当5＜t≤10时，由题意得：，

解得：t＝5（舍去），

综上，当t＝5s时，的面积为正方形面积的．

关闭