
【题目】“![]() 年冬季越野赛”在滨河学校操场举行,某运动员从起点学校东门出发,途径湿地公园,沿比赛路线跑回终点学校东门.沿该运动员离开起点的路程
年冬季越野赛”在滨河学校操场举行,某运动员从起点学校东门出发,途径湿地公园,沿比赛路线跑回终点学校东门.沿该运动员离开起点的路程![]() (千米)与跑步时间
(千米)与跑步时间![]() (时间)之间的函数关系如图所示,其中从起点到湿地公园的平均速度是
(时间)之间的函数关系如图所示,其中从起点到湿地公园的平均速度是![]() 千米/分钟,用时
千米/分钟,用时![]() 分钟,根据图像提供的信息,解答下列问题:
分钟,根据图像提供的信息,解答下列问题:
(![]() )求图中
)求图中![]() 的值;
的值;
(![]() )组委会在距离起点
)组委会在距离起点![]() 千米处设立一个拍摄点
千米处设立一个拍摄点![]() ,该运动员从第一次过点
,该运动员从第一次过点![]() 到第二次过点
到第二次过点![]() 所用的时间为
所用的时间为![]() 分钟.
分钟.
①求![]() 所在直线的函数解析式;
所在直线的函数解析式;
②该运动员跑完全程用时多少分钟?

【答案】(1)10.5;
(2)①直线![]() 解析式为
解析式为![]() ;②该运动员跑完赛程用时
;②该运动员跑完赛程用时![]() 分钟.
分钟.
【解析】试题分析:根据路程=速度×时间,即可解决(1)的问题;
对于(2)中的①,由(1)确定点A的坐标,再根据两次经过点C的时间得出第二次经过点C的坐标,然后由待定系数法求出直线AB的解析式;
最后令s=0,将其代入①中所得关系式,求出x的值即可解决问题②.
解:(![]() )∵从起点到湿地公园的平均速度是
)∵从起点到湿地公园的平均速度是![]() 千米/分,用时
千米/分,用时![]() 分钟,
分钟,
∴![]() 千米.
千米.
(![]() )①∵线段
)①∵线段![]() 经过点
经过点![]() ,
, ![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
∴当![]() 时,
时, ![]() ,解得
,解得![]() ,
,
∵该运动员从第一次经过![]() 点到第二次经过
点到第二次经过![]() 点所用的时间为
点所用的时间为![]() 分钟,
分钟,
∴该运动员从起点到第二次经过![]() 点所用的时间是,
点所用的时间是,
![]() 分钟,
分钟,
∴直线![]() 经过
经过![]() ,
, ![]() ,
,
设直线![]() 解析式
解析式![]() ,
,
∴![]() 解得
解得![]() ,
,
∴直线![]() 解析式为
解析式为![]() .
.
②该运动员跑完赛程用的时间即为直线![]() 与
与![]() 轴交点的横坐标,
轴交点的横坐标,
∴当![]() 时,
时, ![]() ,解得
,解得![]() ,
,
∴该运动员跑完赛程用时![]() 分钟.
分钟.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() ,
,![]() 分别从
分别从![]() ,
,![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动.
时,另一点也随之停止运动.

(1)设![]() 的面积为
的面积为![]() ,
,![]() 为运动时间,写出
为运动时间,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)![]() 为何值时,
为何值时,![]() 的面积为正方形
的面积为正方形![]() 面积的
面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题.
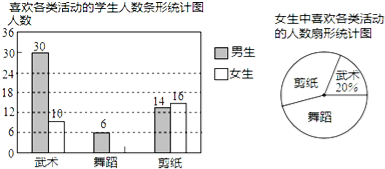
(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是 ;
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD,垂足为E,AD=8,
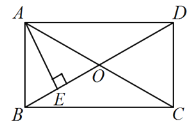
(1)若∠DAE︰∠BAE=3︰1,求∠EAC的度数;
(2)若ED=3BE,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)若该学校共有3600名学生,试估计该校最想去湿地公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠A=(90+x)°,∠B=(90﹣x)°,∠CED=90°,射线EF∥AC,2∠C﹣∠D=m.(1)判断AC与BD的位置关系,并说明理由.
(2)如图1,当m=30°时,求∠C、∠D的度数.
(3)如图2,求∠C、∠D的度数(用含m的代数式表示).
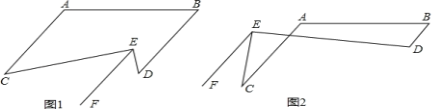
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤![]() PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
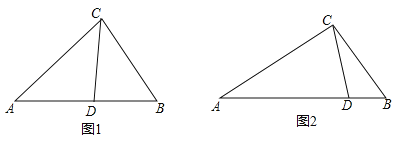
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com