Question

【题目】从三角形（不是等腰三角形）一个顶点引出一条射线于对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．

（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．

（3）如图2，△ABC中，AC=2，BC=，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．

Answer 1

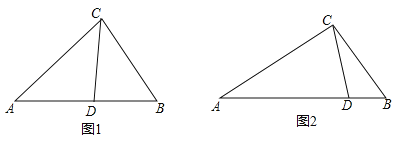
【答案】（1）证明见解析；（2）∠ACB=96°或114°；（3）．

【解析】试题分析：（1）根据完美分割线的定义只要证明①△ABC不是等腰三角形，②△ACD是等腰三角形，③△BDC∽△BCA即可．

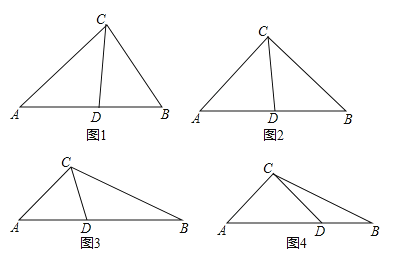
（2）分三种情形讨论即可①如图2，当AD=CD时，②如图3中，当AD=AC时，③如图4中，当AC=CD时，分别求出∠ACB即可．

（3）设BD=x，利用△BCD∽△BAC，得，列出方程即可解决问题．

（1）如图1中，∵∠A=40°，∠B=60°，∴∠ACB=80°，∴△ABC不是等腰三角形，∵CD平分∠ACB，∴∠ACD=∠BCD=∠ACB=40°，∴∠ACD=∠A=40°，∴△ACD为等腰三角形，∵∠DCB=∠A=40°，∠CBD=∠ABC，∴△BCD∽△BAC，∴CD是△ABC的完美分割线．

（2）①当AD=CD时，如图2，∠ACD=∠A=45°，∵△BDC∽△BCA，∴∠BCD=∠A=48°，∴∠ACB=∠ACD+∠BCD=96°．

②当AD=AC时，如图3中，∠ACD=∠ADC=（180°-48°）÷2=66°，∵△BDC∽△BCA，∴∠BCD=∠A=48°，∴∠ACB=∠ACD+∠BCD=114°．

③当AC=CD时，如图4中，∠ADC=∠A=48°，∵△BDC∽△BCA，∴∠BCD=∠A=48°，∵∠ADC＞∠BCD，矛盾，舍弃，∴∠ACB=96°或114°．

（3）由已知AC=AD=2，∵△BCD∽△BAC，∴ 设BD=x，∴），∵x＞0，∴x=，∵△BCD∽△BAC，∴=，∴CD=×2=．