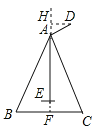
【题目】如图1是一种广场三联漫步机，其侧面示意图如图2所示，其中AB＝AC＝120cm，BC＝80cm，AD＝30cm，∠DAC＝90°．求点D到地面的高度是多少？
【答案】D到地面的高度为（10+80
）cm.
【解析】试题分析：首先过A作AF⊥BC，垂足为F，过点D作DH⊥AF，垂足为H．进而得出AF的长，再利用相似三角形的判定与性质得出AH的长即可得出答案．
试题解析：解：过A作AF⊥BC，垂足为F，过点D作DH⊥AF，垂足为H，
∵AF⊥BC，垂足为F，∴BF=FC=
BC=40cm．
根据勾股定理，得AF=
=80
（cm）．
∵∠DHA=∠DAC=∠AFC=90°，∴∠DAH+∠FAC=90°，∠C+∠FAC=90°，∴∠DAH=∠C，∴△DAH∽△ACF，∴ 
，∴AH=10cm，∴HF=（10+80
）cm．
答：D到地面的高度为（10+80
）cm．
科目：初中数学 来源： 题型：
【题目】已知矩形ABCD中，对角线AC、BD相交于点O，AE⊥BD，垂足为E，AD=8,
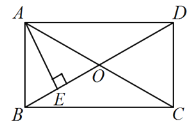
(1)若∠DAE︰∠BAE=3︰1，求∠EAC的度数；
(2)若ED=3BE，求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB＝90，AC＝BC＝2，E、F为线段AB上两动点，且∠ECF＝45°，过点E、F分别作BC、AC的垂线相交于点D，垂足分别为H、G．现有以下结论：①当点E与点B重合时，DH＝1；②GF＋EH＝EF；③AF2＋BE2＝EF2；④DGDH＝2，其中正确结论为（ ）
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．
（1）求证：CD是⊙O的切线；
（2）过点B作⊙O的切线交CD的延长线于点E，BC=6， 
．求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从三角形（不是等腰三角形）一个顶点引出一条射线于对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．
（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．
（3）如图2，△ABC中，AC=2，BC=
，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．
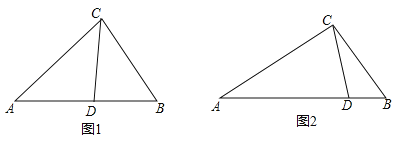
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD∥BC，连接BD，点E在BC上，点F在DC上，连接EF，且∠1＝∠2．
(1)求证：EF∥BD；
(2)若BD平分∠ABC，∠A=130°，∠C＝70°，求∠CFE的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
