
【题目】如图,在△ABC中,∠ACB=90,AC=BC=2,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点D,垂足分别为H、G.现有以下结论:①当点E与点B重合时,DH=1;②GF+EH=EF;③AF2+BE2=EF2;④DGDH=2,其中正确结论为( )

A. ①②③ B. ①③④ C. ①②④ D. ①②③④
【答案】B
【解析】试题解析:解:①如图1,当点E与点B重合时,点H与点B重合,∴DB⊥BC,∠DBC=90°,∵DG⊥AC,∴∠DGC=90°=∠ACB=∠DBC,∴DG∥BC,四边形DGCB是矩形,∴DH=DB=CG,∵∠FCE=45°=∠ABC,∠A=∠ACF=45°,∴CE=AF=BF,∴FG是△ACB的中位线,∴GC=![]() AC=DH,故①正确;
AC=DH,故①正确;
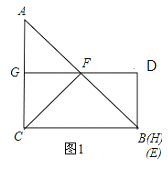
②如果CG=CH或者GCHD是正方形,如图,把△ECH绕点C逆时针旋转90°,得到△MCG,则MC=CE,∠MCG=∠ECH,∵∠ACB=90°,∠ECF=45°,∴∠GCF+∠ECH=45°,∴∠GCF+∠MCG=45°,∴∠MCF=∠FCE=45°,在△MCF和△ECF中,∵MC=EC,∠MCF=∠ECF,CF=CF,∴△MCF≌△ECF,∴MF=EF,∴MG+FG=EF,∴EH+GF=EF.
一般情况下,CG≠CH或者GCHD不是正方形,故②错误;

③如图2所示,∵AC=BC,∠ACB=90°,∴∠A=∠5=45°.
将△ACF顺时针旋转90°至△BCK,则CF=CK,∠1=∠4,∠A=∠6=45°;BK=AF;
∵∠2=45°,∴∠1+∠3=∠3+∠4=45°,∴∠KCE=∠2.
在△ECF和△ECK中,CF=CK,∠2=∠KCE,CE=CE,∴△ECF≌△ECK(SAS),∴EF=KE.
∵∠5=45°,∴∠BKE=90°,∴KE2=BK2+BE2,即EF2=AF2+BE2,故③正确;
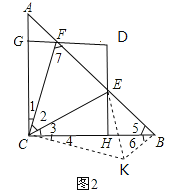
④∵∠7=∠1+∠A=∠1+45°=∠1+∠2=∠ACE,∵∠A=∠5=45°,∴△ACE∽△BFC,∴ ![]() ,∴AEBF=ACBC=4,由题意知四边形CHDG是矩形,∴DG∥BC,DH=CG, DH∥AC,∴
,∴AEBF=ACBC=4,由题意知四边形CHDG是矩形,∴DG∥BC,DH=CG, DH∥AC,∴![]() ;
; ![]() ,即
,即![]() ;
; ![]() ,∴DG=
,∴DG=![]() AE;DH=
AE;DH=![]() BF,∴DGDH=
BF,∴DGDH=![]() AE×
AE×![]() BF=
BF=![]() AEBF=
AEBF=![]() ACBC=2,故④正确.
ACBC=2,故④正确.
故答案为:①③④.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,AD=6,点E在AD边上,且AE=4,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
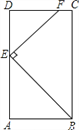
【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
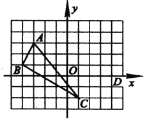
【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标: A′(_____,______); B′(_____,______); C′(_____,______)。
(3)求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, ![]() ,
, ![]() ∥
∥![]() 轴,
轴, ![]() .
.

⑴.求点![]() 的坐标:
的坐标:
⑵.四边形![]() 的面积
的面积![]() 四边形
四边形![]() ;
;
⑶. 在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() △
△![]() =
= ![]() 四边形
四边形![]() ;若存在,求出点
;若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种广场三联漫步机,其侧面示意图如图2所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件不能判定四边形ABCD是矩形的是( )

A.∠DAB=∠ABC=∠BCD=90°B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DOD.AO=BO=CO=DO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现计划把1240吨甲种货物和880吨乙种货物用一列火车运往某地,已知这列火车挂有A、B两种不同规格的货车车厢共40节,使用A型车厢每节费用为6000元,B型车厢每节费用8000元.如果每节A型车厢最多可装35吨甲种货物和15吨乙种货物,每节B型车厢最多可装25吨甲种货物和35吨乙种货物;
(1)那么共有哪几种安排车厢的方案?
(2)在上述方案中,哪种方案运费最省、最少运费为多少元?
(3)在(1)问下,若两种货物全部售出,且每吨货物售出获利200元,除去运费获
利154000元,问:在这种情况下是按哪种方案安排车厢的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com