
【题目】已知矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD,垂足为E,AD=8,
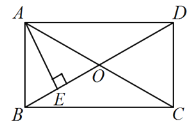
(1)若∠DAE︰∠BAE=3︰1,求∠EAC的度数;
(2)若ED=3BE,求AE的长.
【答案】(1)45°;(2)4.
【解析】
(1)由已知条件求出∠BAE=22.5°,再根据矩形的性质得到OA=OB,求出∠OAB=∠ABE=67.5°,即可得出∠EAC的度数;
(2)根据矩形的性质和等腰三角形三线合一的性质得到△OAB是等边三角形,求出∠ADE =30°,利用含30°角的直角三角形的性质可求出AE.
(1)解:∵∠DAE︰∠BAE=3︰1,
∴∠BAE=90°×![]() =22.5°,
=22.5°,
∴∠ABE=67.5°,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO
∴OA=OB,
∴∠OAB=∠ABE=67.5°
∴∠EAC=∠OAB![]() ∠BAE=67.5°
∠BAE=67.5°![]() 22.5°=45°;
22.5°=45°;
(2)∵OA=OB=OD,ED=3BE,
∴OE+OD=3BE,
∴OB![]() BE+OB=3BE,
BE+OB=3BE,
∴OB =2BE,
∴点E为OB的中点,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,即△OAB是等边三角形,
∴∠ABD=60°,
∴∠ADE=90°![]() ∠ABD=30°,
∠ABD=30°,
∵AE⊥BD,AD=8,
∴AE=![]() AD=4.
AD=4.


科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(![]() )﹣2﹣(﹣2)0+(﹣0.2)2018×(﹣5)2018;
)﹣2﹣(﹣2)0+(﹣0.2)2018×(﹣5)2018;
(2)用整式乘法公式计算:1012﹣1;
(3)(x2y+2x2y﹣y3)÷y﹣(y+2x)(2x﹣y);
(4)先化简,再求值:(a﹣2b)2+(a﹣b)(a+b)﹣2(a﹣3b)(a﹣b),其中,a=1,b=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
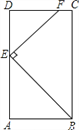
【题目】如图,在矩形ABCD中,AB=3,AD=6,点E在AD边上,且AE=4,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
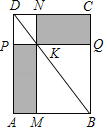
【题目】如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2;(填“>”或“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“![]() 年冬季越野赛”在滨河学校操场举行,某运动员从起点学校东门出发,途径湿地公园,沿比赛路线跑回终点学校东门.沿该运动员离开起点的路程
年冬季越野赛”在滨河学校操场举行,某运动员从起点学校东门出发,途径湿地公园,沿比赛路线跑回终点学校东门.沿该运动员离开起点的路程![]() (千米)与跑步时间
(千米)与跑步时间![]() (时间)之间的函数关系如图所示,其中从起点到湿地公园的平均速度是
(时间)之间的函数关系如图所示,其中从起点到湿地公园的平均速度是![]() 千米/分钟,用时
千米/分钟,用时![]() 分钟,根据图像提供的信息,解答下列问题:
分钟,根据图像提供的信息,解答下列问题:
(![]() )求图中
)求图中![]() 的值;
的值;
(![]() )组委会在距离起点
)组委会在距离起点![]() 千米处设立一个拍摄点
千米处设立一个拍摄点![]() ,该运动员从第一次过点
,该运动员从第一次过点![]() 到第二次过点
到第二次过点![]() 所用的时间为
所用的时间为![]() 分钟.
分钟.
①求![]() 所在直线的函数解析式;
所在直线的函数解析式;
②该运动员跑完全程用时多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种广场三联漫步机,其侧面示意图如图2所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com