
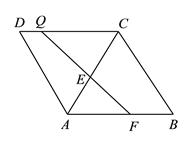
【题目】如图,菱形![]() 的边
的边![]() ,
, ![]() ,
, ![]() 是
是![]() 上一点,
上一点, ![]() ,
, ![]() 是
是![]() 边上一动点,将梯形
边上一动点,将梯形![]() 沿直线
沿直线![]() 折叠,
折叠, ![]() 的对应点为
的对应点为![]() ,当
,当![]() 的长度最小时,
的长度最小时, ![]() 的长为__________.
的长为__________.
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
中华优秀传统文化是中华民族的“根”和“魂”,是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化,某校为各班购进《三国演义》和《水浒传》连环画若干套,其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元,用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍,求每套《水浒传》连环画的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)
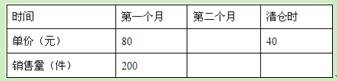
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD,垂足为E,AD=8,
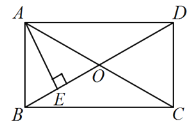
(1)若∠DAE︰∠BAE=3︰1,求∠EAC的度数;
(2)若ED=3BE,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
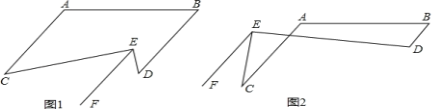
【题目】已知:∠A=(90+x)°,∠B=(90﹣x)°,∠CED=90°,射线EF∥AC,2∠C﹣∠D=m.(1)判断AC与BD的位置关系,并说明理由.
(2)如图1,当m=30°时,求∠C、∠D的度数.
(3)如图2,求∠C、∠D的度数(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图①,直线AB∥CD,E是AB与CD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
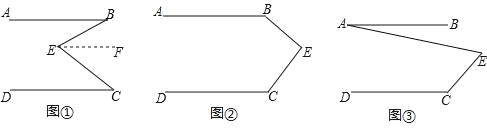
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( )
∴∠C=∠CEF.( )
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C= (等式性质)
即∠B+∠C=∠BEC.
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,求证:∠B+∠C=360°﹣∠BEC.
(3)解决问题:如图③,AB∥DC,试写出∠A、∠C、∠AEC的数量关系 .(直接写出结论,不用写计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com