【题目】如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE=DF．
（1）求证：AE=CF；
（2）若AB=6，∠COD=60°，求矩形ABCD的面积．
【答案】
【解析】试题分析：（1）由矩形的性质得出OA=OC，OB=OD，AC=BD，∠ABC=90°，证出OE=OF，由SAS证明△AOE≌△COF，即可得出AE=CF；
（2）证出△AOB是等边三角形，得出OA=AB=6，AC=2OA=12，在Rt△ABC中，由勾股定理求出BC的长，即可得出矩形ABCD的面积．
试题解析：（1）证明：∵四边形ABCD是矩形，∴OA=OC，OB=OD，AC=BD，∠ABC=90°，∵BE=DF，∴OE=OF，在△AOE和△COF中，∵OA=OC，∠AOE=∠COF，OE=OF，∴△AOE≌△COF（SAS），∴AE=CF；
（2）解：∵OA=OC，OB=OD，AC=BD，∴OA=OB，∵∠AOB=∠COD=60°，∴△AOB是等边三角形，∴OA=AB=6，∴AC=2OA=12，在Rt△ABC中，BC=
=
，∴矩形ABCD的面积=ABBC=6×=
．
科目：初中数学 来源： 题型：
【题目】如图，已知原点为
的数轴上，点
表示的数为-7，点
表示的数为5．
（1）若数轴上点
到点，点的距离相等，求点表示的数；
（2）若数轴上点
到点，到点的距离之比为
，求点表示的数；
（3）若一动点
从点以每秒1个单位长度沿数轴向左匀速运动，同时动点
从点出发，以每秒3个单位长度沿数轴向左匀速运动，设运动的时间为
秒
，
之间的距离为8个单位长度时，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠A=60°，BE⊥AC，垂足为E，CF⊥AB，垂足为F，点D是BC的中点，BE，CF交于点M，如果CM=4，FM=5，则BE等于( )
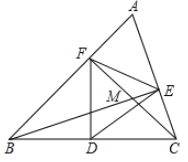
A. 14B. 13C. 12D. 11
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标中，点
为坐标原点，
的三个顶点坐标分别为
，
，
，
且
，其中
，
满足
．
（1）求点
，
的坐标；
（2）点
从点出发，以每秒1个单位长度的速度沿
轴负方向运动，设点的运动时间为
秒.连接
、
，用含有的式子表示
的面积为
（直接写出的取值范围）；
（3）在（2）的条件下，是否存在的值，使得
，若存在，请求出的值，并直接写出中点
的坐标；若不存，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球．
（1）求从袋中摸出一个球是黄球的概率；
（2）现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是 
，求从袋中取出黑球的个数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，AD∥BC，AB⊥AC，点E是BC的中点，AE与BD交于点F，且F是AE的中点．
（Ⅰ）求证：四边形AECD是菱形；（Ⅱ）若AC＝4，AB＝5，求四边形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设直线y＝kx+6和直线y＝（k+1）x+6（k是正整数）及x轴围成的三角形面积为Sk（k＝1，2，3，…，8），则S1+S2+S3+…+S8的值是（ ）
A. 
B. 
C. 16D. 14
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使AB=AC，连结AC，过点D作DE⊥AC，垂足为E．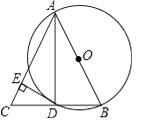
（1）求证：DC=BD；
（2）求证：DE为⊙O的切线．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
