
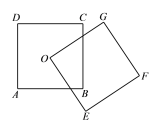
【题目】如图所示,正方形ABCD和正方形OEFG的边长均为5,O为正方形ABCD的中心,则图中重叠部分的面积是 _______.
【答案】![]()
【解析】
如图,连接OB、OC,根据正方形的对角线相等且互相平分可得OB=OC,再根据两角的和等于90°可以证明∠COH=∠BOG,又∠OBG=∠OCB=45°,证明△OBG与△OCH全等,从而得到重叠部分的面积等于△OBC的面积,即正方形的面积的![]() .
.
如图,连接OB、OC.
∵O为正方形ABCD的中心,∴OB=OC,∠OBG=∠OCB=45°.
∵∠COH+∠BOH=90°,∠BOG+∠BOH=90°,∴∠COH=∠BOG.
在△OBG与△OCH中,∵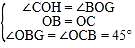 ,∴△OBG≌△OCH(ASA),∴S△OBG=S△OCH,∴重叠部分的面积=△OBC的面积
,∴△OBG≌△OCH(ASA),∴S△OBG=S△OCH,∴重叠部分的面积=△OBC的面积![]() S正方形ABCD.
S正方形ABCD.
∵S正方形ABCD=52=25,∴重叠部分的面积是![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】“拼图,推演,得到了整式的乘法的法则和乘法公式.教材第9章头像拼图这样,借助图形往往能把复杂的数学问题变得简明、形象.
(分数运算)
怎样理解![]() ?
?

从图形的变化过程可以看出,长方形先被平均分成3份,取其中的2份(涂![]() 部分);再将涂色部分平均分成5份,取其中4份(涂
部分);再将涂色部分平均分成5份,取其中4份(涂![]() 部分).这样,可看成原长方形被平均分成15份,取出其中8份,所以
部分).这样,可看成原长方形被平均分成15份,取出其中8份,所以![]() 的
的![]() 占原长方形的
占原长方形的![]() ,即
,即![]() .
.
(尝试推广)
(1)①类比分数运算,猜想![]() 的结果是____________;(a、b、c、d均为正整数,且
的结果是____________;(a、b、c、d均为正整数,且![]() ,
,![]() );
);
②请用示意图验证①的猜想并用文字简单解释.
(2)①观察下图,填空:![]() ____________;
____________;

②若a、b均为正整数且![]() ,猜想
,猜想![]() 的运算结果,并用示意图验证你的猜想,同时加以简单的文字解释.
的运算结果,并用示意图验证你的猜想,同时加以简单的文字解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从学校出发,沿相同的线路跑向公园.甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度继续跑向公园.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)之间函数关系的图象,根据题意填空:
(1)在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;
(2)乙最早出发时跑步的速度为 米/秒,乙在途中等候甲的时间为 秒;
(3)乙出发 秒后与甲第一次相遇.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情爆发以来,学生们都在家里上网课,为了了解学生在家上网课使用的设备种类,47中学校初二学年在本学年内随机抽取部分学生进行问卷调查,要求学生在“台式电脑、笔记本电脑、平板电脑、手机、网络电视”五类设备中,选取自己经常使用的一种(必选且只选一种),学年将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:

(1)在这次调查中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图;
(3)若47中学初二学年共有1000名学生,估计该校初二学年使用手机上课的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,点G为边BC的中点,点D从点C出发沿CA向点A运动,到点A停止,以GD为边作正方形DEFG,则点E运动的路程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副直角三角尺叠放如图 1 所示,现将 45°的三角尺ADE 固定不动,将含 30°的三角尺 ABC 绕顶点 A 顺时针转动(旋转角不超过 180 度),使两块三角尺至少有一组边互相平行.如图 2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用格点和三角尺画图:
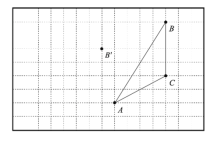
(1)补全△A′B′C′;
(2)请在AC边上找一点D,使得线段BD平分△ABC的面积,在图上作出线段BD;
(3)利用格点在图中画出AC边上的高线BE;
(4)求△ABD的面积_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com