
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】
试题已知△ABC、△DCE为正三角形, 故∠DCE=∠BCA=60°,∴∠DCB=60°,
又因为∠DPC=∠DAC+∠BCA,∠BCA=60°,∴∠DPC>60°, 故DP不等于DE,④错.
∵△ABC、△DCE为正三角形, ∴∠ACB=∠DCE=60°,AC=BC,DC=EC, ∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE, ∴△ACD≌△BCE(SAS), ∴∠CAD=∠CBE,AD=BE,故①正确;
∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB, ∵∠ACB=∠CBE+∠CEB=60°, ∴∠AOB=60°,故⑤正确;
∵∠ACB=∠DCE=60°, ∴∠BCD=60°, ∴∠ACP=∠BCQ, ∵AC=BC,∠DAC=∠QBC,
∴△ACP≌△BCQ(ASA), ∴AP=BQ,故③正确.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )

A. 3 B. 4 C. 3.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走1.5 km,遇到障碍后又往西走2 km,再折回向北走到4.5 km处往东一拐,仅走0.5 km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?
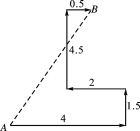
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求画图,并回答问题.
已知:直线AB,CD相交于点O,且OE⊥AB.
(1)过点O画直线MN⊥CD;
(2)若点F是(1)中所画直线MN上任意一点(O点除外),若∠AOC=35°,求∠EOF的度数.
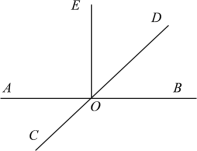
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E. 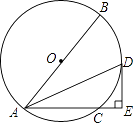
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4cm,BC=8cm.点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→D→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了3cm,并沿B→C→D→A的路径匀速运动;点Q保持速度不变,继续沿原路径匀速运动,3s后两点在长方形ABCD某一边上的E点处第二次相遇后停止运动.设点P原来的速度为xcm/s.

(1)点Q的速度为 cm/s(用含x的代数式表示);
(2)求点P原来的速度.
(3)判断E点的位置并求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州苍南马站四季柚,声名远播,今年又是一个丰收年,某经销商为了打开销路,对1 000个四季柚进行打包优惠出售.打包方式及售价如图所示.假设用这两种打包方式恰好装完全部柚子.
(1)若销售a箱纸盒装和a袋编织袋装四季柚的收入共950元,求a的值;
(2)当销售总收入为7 280元时:
①若这批四季柚全部售完,请问纸盒装共包装了多少箱,编织袋装共包装了多少袋.
②若该经销商留下b(b>0)箱纸盒装送人,其余柚子全部售出,求b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一幅三角板摆放在一起.
(1)∠AOC的度数为________,射线OA 、OB、OC组成所有小于平角的和为________;
(2)反向延长射线OA 到D,OE为∠BOD的平分线,OF为∠COD的平分线,请按题意画出图形,并求出∠EOF的度数.
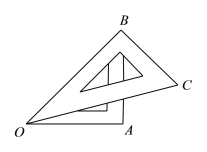
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com