
ЁОЬтФПЁПЮТжнВдФЯТэеОЫФМОшжЃЌЩљУћдЖВЅЃЌНёФъгжЪЧвЛИіЗсЪеФъЃЌФГОЯњЩЬЮЊСЫДђПЊЯњТЗЃЌЖд1 000ИіЫФМОшжНјааДђАќгХЛнГіЪлЃЎДђАќЗНЪНМАЪлМлШчЭМЫљЪОЃЎМйЩшгУетСНжжДђАќЗНЪНЧЁКУзАЭъШЋВПшжзгЃЎ
(1)ШєЯњЪлaЯфжНКазАКЭaДќБржЏДќзАЫФМОшжЕФЪеШыЙВ950дЊЃЌЧѓaЕФжЕЃЛ
(2)ЕБЯњЪлзмЪеШыЮЊ7 280дЊЪБЃК
ЂйШєетХњЫФМОшжШЋВПЪлЭъЃЌЧыЮЪжНКазАЙВАќзАСЫЖрЩйЯфЃЌБржЏДќзАЙВАќзАСЫЖрЩйДќЃЎ
ЂкШєИУОЯњЩЬСєЯТb(b>0)ЯфжНКазАЫЭШЫЃЌЦфгршжзгШЋВПЪлГіЃЌЧѓbЕФжЕЃЎ

ЁОД№АИЁП(1) aЃН5ЃЛ(2)ЂйжНКазАЙВАќзАСЫ35ЯфЃЌБржЏДќзАЙВАќзАСЫ40ДќЃЛЂкbЮЊ9.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЪеШыЙВ950дЊЃЌПЩЕУГівЛдЊвЛДЮЗНГЬЃЌНтГіМДПЩЃЛ
ЃЈ2ЃЉЂйжНКазАЙВАќзАСЫxЯфЃЌдђБржЏДќзАЙВАќзАy ДќЃЌИљОнЕШСПЙиЯЕПЩЕУГіЗНГЬзщЃЌНтГіМДПЩЃЛЂкИљОнЂйЕФЙиЯЕПЩвдyБэЪОГіxЃЌМѕШЅСєЯТЕФbЯфжНКазАЃЌдйгЩЯњЪлзмЪеШыЮЊ7280дЊЃЌПЩЕУГіЗНГЬЃЌНтГіМДПЩЃЎ
(1)гЩЬтвтЕУ64aЃЋ126aЃН950ЃЌЕУaЃН5.
(2)ЂйЩшжНКазАЙВАќзАСЫxЯфЃЌБржЏДќзАЙВАќзАСЫyДќЃЎ
гЩЬтвтЕУ![]()
НтЕУ![]()
ЁржНКазАЙВАќзАСЫ35ЯфЃЌБржЏДќзАЙВАќзАСЫ40ДќЃЎ
ЂкЕБ8xЃЋ18yЃН1 000ЪБЃЌЕУxЃН![]() ЃН125Ѓ
ЃН125Ѓ![]() ЃЌгЩЬтвтЕУ64
ЃЌгЩЬтвтЕУ64![]() ЃЋ126yЃН7 280ЃЌЕУyЃН40Ѓ
ЃЋ126yЃН7 280ЃЌЕУyЃН40Ѓ![]() .
.
ЁпxЃЌyЃЌbЖМЮЊећЪ§ЃЌЧвxЁн0ЃЌyЁн0ЃЌbЃО0ЃЌ
ЁрbЃН9ЃЌxЃН107ЃЌyЃН8.ЁрbЮЊ9.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪЎАЫЪРМЭШ№ЪПЪ§бЇМвХЗРжЄУїСЫМђЕЅЖрУцЬхжаЖЅЕуЪ§ЃЈVЃЉЁЂУцЪ§ЃЈFЃЉЁЂРтЪ§ЃЈEЃЉжЎМфДцдкЕФвЛИігаШЄЕФЙиЯЕЪНЃЌЧыФуЙлВьЯТСаМИжжМђЕЅЖрУцЬхФЃаЭЃЌНтД№ЯТСаЮЪЬтЃК

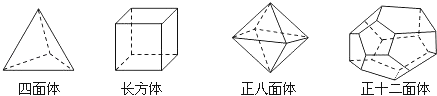
ЭМ1 ЭМ2
ЃЈЬНЫїаТжЊЃЉШчЭМ1ЃЌЃЈ1ЃЉИљОнЩЯУцЖрУцЬхФЃаЭЃЌЭъГЩБэИёжаЕФПеИёЃЛ
ЖрУцЬх | ЖЅЕуЪ§ЃЈVЃЉ | УцЪ§ЃЈFЃЉ | РтЪ§ЃЈEЃЉ |
ЫФУцЬх | 4 | 4 | |
ГЄЗНЬх | 8 | 6 | 12 |
е§АЫУцЬх | 8 | 12 | |
е§ЪЎЖўУцЬх | 20 | 12 | 30 |
ФуЗЂЯжЖЅЕуЪ§ЃЈVЃЉЁЂУцЪ§ЃЈFЃЉЁЂРтЪ§ЃЈEЃЉжЎМфДцдкЕФЙиЯЕЪНЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉИљОнвдЩЯЙиЯЕЪНВТЯыЪЧЗёДцдквЛИіЖрУцЬхЃЌЫќга16ИіУцЃЌ50ЬѕРтЃЌ34ИіЖЅЕуЃПВЂаДГіРэгЩЁЃ
ЃЈЪЕМЪгІгУЃЉШчЭМ2ЃЌзуЧђвЛАуга32ПщКкАзЦЄзгЗьКЯЖјГЩЃЌКкЩЋЕФЪЧе§ЮхБпаЮЃЌАзЩЋЕФЪЧе§СљБпаЮЃЌШч
ЙћЮвУЧНќЫЦАбзуЧђПДГЩвЛИіЖрУцЬхЃЎ
ЃЈ1ЃЉЩшКкЩЋЕФе§ЮхБпаЮгаxПщЃЌдђАзЩЋЕФе§СљБпаЮгаЃЈ32ЉxЃЉПщЃЌЕБАбзуЧђПДГЩвЛИіЖрУцЬхЪБЃЌЫќЕФРтЪ§ЪЧ ЁЁЃЌЫќЕФЖЅЕуЪ§ЪЧ ЁЁЃЎ
ЃЈ2ЃЉЧѓГіКкЦЄКЭАзЦЄИїгаЖрЩйПщЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌCЮЊЯпЖЮAEЩЯвЛЖЏЕуЃЈВЛгыЕуAЃЌEжиКЯЃЉЃЌдкAEЭЌВрЗжБ№зїЕШБпЁїABCКЭЕШБпЁїCDEЃЌADгыBEНЛгкЕуOЃЌADгыBCНЛгкЕуPЃЌBEгыCDНЛгкЕуQЃЌСЌНгPQЃЎвдЯТЮхИіНсТлЃК

ЂйAD=BEЃЛЂкPQЁЮAEЃЛЂлAP=BQЃЛЂмDE=DPЃЛ ЂнЁЯAOB=60ЁуЃЎ
Цфжае§ШЗЕФНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
A. 2Иі B. 3Иі C. 4Иі D. 5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌCDЪЧЁЯACBЕФНЧЦНЗжЯпЃЌЕуEЃЌFЗжБ№ЪЧБпACЃЌ BCЩЯЕФЖЏЕуЃЌAC=4ЃЌЩшAE=xЃЌBF=yЃЎ
ЃЈ1ЃЉШєx+y=3ЃЌЧѓЫФБпаЮCEDFЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕБDEЁЭDFЪБЃЌШчЭМ2ЃЌЪдЬНЫїxЁЂyжЎМфЕФЪ§СПЙиЯЕЃЎ
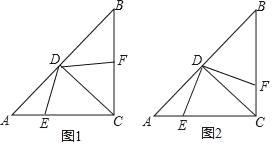
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПAЁЂBЁЂC ЮЊЪ§жсЩЯШ§ЕуЃЌШєЕу C ЕНЕу A ЕФОрРыЪЧЕу C ЕНЕу B ЕФОрРыЕФ 2БЖЃЌдђГЦЕу C ЪЧЃЈAЃЌBЃЉЕФЦцвьЕуЃЌР§ШчЭМ 1 жаЃЌЕу A БэЪОЕФЪ§ЮЊЉ1ЃЌЕуB БэЪОЕФЪ§ЮЊ 2ЃЌБэЪО 1 ЕФЕу C ЕНЕу A ЕФОрРыЮЊ 2ЃЌЕНЕу B ЕФОрРыЮЊ 1ЃЌдђЕуC ЪЧЃЈAЃЌBЃЉЕФЦцвьЕуЃЌЕЋВЛЪЧЃЈBЃЌAЃЉЕФЦцвьЕуЃЎ
(1)дкЭМ 1 жаЃЌжБНгЫЕГіЕу D ЪЧЃЈAЃЌBЃЉЛЙЪЧЃЈBЃЌCЃЉЕФЦцвьЕуЃЛ
(2)ШчЭМ 2ЃЌШєЪ§жсЩЯ MЁЂN СНЕуБэЪОЕФЪ§ЗжБ№ЮЊЉ2 КЭ 4ЃЌЃЈMЃЌNЃЉЕФЦцвьЕу K дк MЁЂN СНЕужЎМфЃЌЧыЧѓГі K ЕуБэЪОЕФЪ§ЃЛ
(3)ШчЭМ 3ЃЌAЁЂB дкЪ§жсЩЯБэЪОЕФЪ§ЗжБ№ЮЊЉ20 КЭ 40ЃЌЯжгавЛЕу P ДгЕу B ГіЗЂЃЌЯђзѓдЫЖЏЃЎ
ЂйШєЕу P ЕНДяЕу A ЭЃжЙЃЌдђЕБЕу P БэЪОЕФЪ§ЮЊЖрЩйЪБЃЌPЁЂAЁЂB жаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФЦцвьЕуЃП
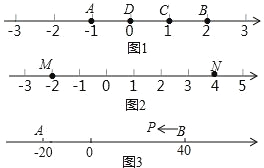
ЂкШєЕу P ЕНДяЕу A КѓМЬајЯђзѓдЫЖЏЃЌЪЧЗёДцдкЪЙЕУ PЁЂAЁЂB жаЧЁгавЛИіЕуЮЊЦфгрСНЕуЕФЦцвьЕуЕФЧщПіЃПШєДцдкЃЌЧыжБНгаДГіДЫЪБ PB ЕФОрРыЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПелЕўОиаЮABCDЕФвЛБпADЃЌЪЙЕуDТфдкBCБпЕФFЕуДІЃЌШєAB=8cmЃЌBC=10cmЃЌЧѓECЕФГЄ.
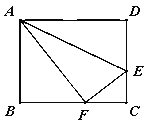
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
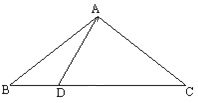
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЁїABCжаЃЌAB=AC=10ЃЌBC=16ЃЌЕуDдкBCЩЯЃЌDAЁЭCAгкAЁЃ
ЧѓЃКBDЕФГЄЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаНтЬтЙ§ГЬЃКЃЈ-15ЃЉЁТЃЈ![]() -3ЃЉЁС6
-3ЃЉЁС6
ЃЈНтЮіЃЉдЪН=ЃЈ-15ЃЉЁТЃЈ-![]() ЃЉЁС6 ЃЈЕквЛВНЃЉ
ЃЉЁС6 ЃЈЕквЛВНЃЉ
=ЃЈ-15ЃЉЁТЃЈ-25ЃЉЃЈЕкЖўВНЃЉ
=-![]() ЃЈЕкШ§ВНЃЉ
ЃЈЕкШ§ВНЃЉ
НтД№ЮЪЬтЃК
ЂйЩЯУцНтД№Й§ГЬгаСНИіДэЮѓЃЌЕквЛДІЪЧЕк______ВНЃЌДэЮѓЕФдвђЪЧ______ЃЛЕкЖўДІЪЧЕк______ВНЃЌДэЮѓЕФдвђЪЧ______ЃЛ
ЂкЧыФуе§ШЗНтД№БОЬтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§y=(m+2)x+3-nЃЌ
(l)mЃЌnЪЧКЮжЕЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃП
(2)mЃЌnЮЊКЮжЕЪБЃЌКЏЪ§ЕФЭМЯѓОЙ§дЕуЃП
(3)ШєКЏЪ§ЭМЯѓОЙ§ЕкЖўЁЂШ§ЁЂЫФЯѓЯоЃЌЧѓ mЃЌnЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com