
【题目】已知一次函数y=(m+2)x+3-n,
(l)m,n是何值时,y随x的增大而减小?
(2)m,n为何值时,函数的图象经过原点?
(3)若函数图象经过第二、三、四象限,求 m,n的取值范围.
【答案】(1)m<-2,n为任意实数时,y随x的增大而减小;(2)当m≠-2且n=3时,图象经过原点;(3)当m<-2且n>3时,函数图象经过第二、三、四象限.
【解析】试题分析:(1)根据一次函数的性质可得m+2<0,对其求解即可;
(2)结合题意可知一次函数是正比例函数,此时结合正比例函数的定义进行解答即可;
(3)根据一次函数的性质列出不等式组,并进行解答即可.
试题解析:
1)由题意得:m+2<0,
∴m<-2,
∴m<-2,n为任意实数时,y随x的增大而减小。
(2)由题意得:m+2≠0且3-n=0,
∴m≠-2且n=3,
∴当m≠-2且n=3时,图象经过原点。
(3)由题意得: ![]() ,
,
得: ![]()
∴当m<-2且n>3时,函数图象经过第二、三、四象限.


科目:初中数学 来源: 题型:
【题目】温州苍南马站四季柚,声名远播,今年又是一个丰收年,某经销商为了打开销路,对1 000个四季柚进行打包优惠出售.打包方式及售价如图所示.假设用这两种打包方式恰好装完全部柚子.
(1)若销售a箱纸盒装和a袋编织袋装四季柚的收入共950元,求a的值;
(2)当销售总收入为7 280元时:
①若这批四季柚全部售完,请问纸盒装共包装了多少箱,编织袋装共包装了多少袋.
②若该经销商留下b(b>0)箱纸盒装送人,其余柚子全部售出,求b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
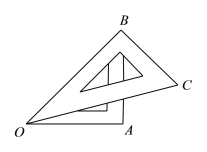
【题目】如图,将一幅三角板摆放在一起.
(1)∠AOC的度数为________,射线OA 、OB、OC组成所有小于平角的和为________;
(2)反向延长射线OA 到D,OE为∠BOD的平分线,OF为∠COD的平分线,请按题意画出图形,并求出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段, ![]() ≈1.414,
≈1.414, ![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 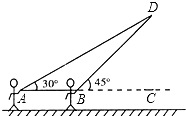
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 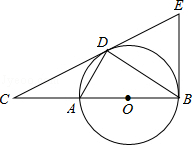
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A=2 x2+3xy﹣2x﹣1,B= x2﹣xy﹣1.
(1)化简:4A﹣(2B+3A),将结果用含有 x、y 的式子表示;
(2)若式子 4A﹣(2B+3A)的值与字母 x 的取值无关,求 y3+![]() A﹣
A﹣ ![]() B 的值.
B 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:为了求1+3+32+33+…+3100的值,可设M=1+3+32+33+…+3100,则3M=3+32+33+34+…+3101,因此3M﹣M=3101﹣1.所以M=![]() ,即1+3+32+33+…+3100=
,即1+3+32+33+…+3100=![]() .问题解决:仿照上述方法求下列式子的值.
.问题解决:仿照上述方法求下列式子的值.
(1)1+4+42+43+…+420.
(2)5101+5102+5103+…+52018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
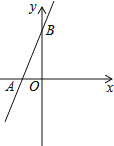
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求直线BP的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com