
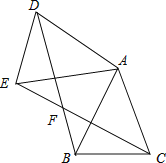
【题目】如图,已知![]() 中,
中,![]() ,把
,把![]() 绕A点沿顺时针方向旋转得到
绕A点沿顺时针方向旋转得到![]() ,连接BD,CE交于点F.
,连接BD,CE交于点F.
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 若
若![]() ,
,![]() ,当四边形ADFC是菱形时,求BF的长.
,当四边形ADFC是菱形时,求BF的长.
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:(-15)÷(![]() -3)×6
-3)×6
(解析)原式=(-15)÷(-![]() )×6 (第一步)
)×6 (第一步)
=(-15)÷(-25)(第二步)
=-![]() (第三步)
(第三步)
解答问题:
①上面解答过程有两个错误,第一处是第______步,错误的原因是______;第二处是第______步,错误的原因是______;
②请你正确解答本题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(m+2)x+3-n,
(l)m,n是何值时,y随x的增大而减小?
(2)m,n为何值时,函数的图象经过原点?
(3)若函数图象经过第二、三、四象限,求 m,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.
(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;
(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州国际动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,动漫公司又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司两次共购进这种玩具多少套?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们运用图(Ⅰ)中大正方形的面积可表示为(a+b)2,也可表示为c3+4(![]() ab),即(a+b)2=c2+4(
ab),即(a+b)2=c2+4(![]() ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
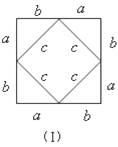
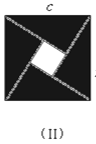
(1)请你用图(Ⅱ)(2002年国际数学家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a,较小的直角边长都为b,斜边长都为c).
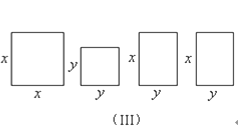
(2)请你用(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:为了求1+3+32+33+…+3100的值,可设M=1+3+32+33+…+3100,则3M=3+32+33+34+…+3101,因此3M﹣M=3101﹣1.所以M=![]() ,
,
即1+3+32+33+…+3100=![]() .问题解决:仿照上述方法求下列式子的值.
.问题解决:仿照上述方法求下列式子的值.
(1)1+4+42+43+…+420.
(2)5101+5102+5103+…+52016.
查看答案和解析>>
科目:初中数学 来源: 题型:
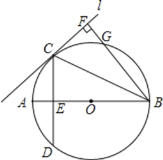
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某商场因换季,将一品牌服装打折销售,每件服装如果按标价的六折出售将亏10元,而按标价的七五折出售将赚50元,问:
(1) 每件服装的标价是多少元?
(2) 每件服装的成本是多少元?
(3)为保证不亏本,最多能打几折?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com